人間は考える葦である?
を唱えた人だと思って調べたらそうだった。
自然の中で最も弱い存在だけど、「考える」ことができるので尊重しよう的な。
あと気圧の単位の「パスカル」もこの人みたい。
ヘクトパスカルとかいうやーつ。
哲学者で物理学者で数学者。
ブレーズ・パスカルさん。
つよ。
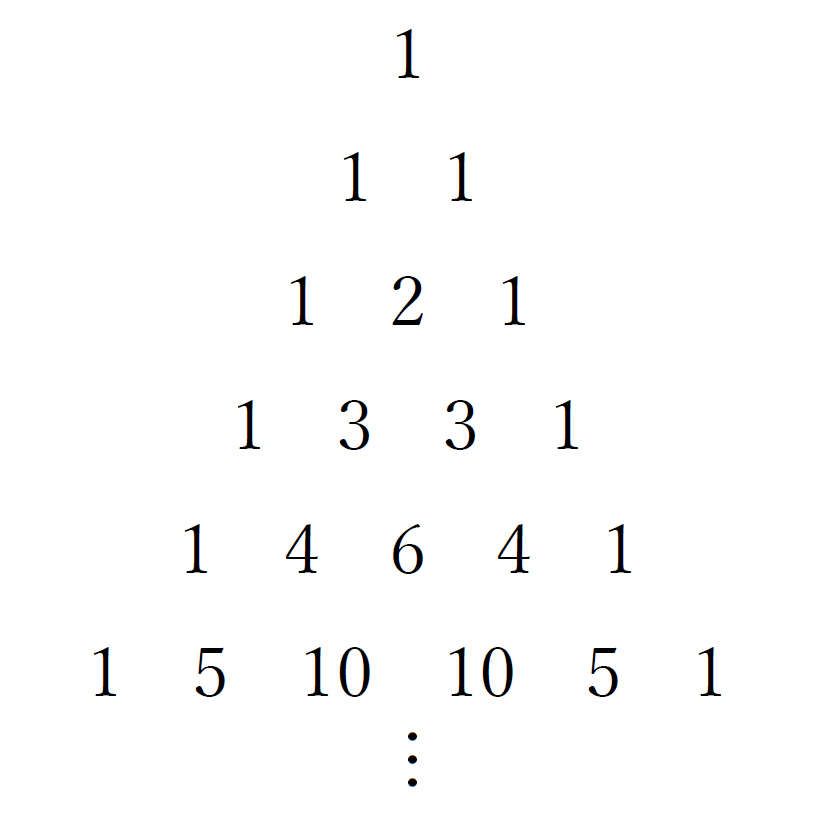
とりあえずこれが「パスカルの三角形」って呼ばれている。
パスカルの三角形とは何なのか。
パスカルの三角形は、二項展開における係数を三角形状に並べたものである。
(Wikipediaより)
まったく分からんね。
1
まず1を書く。
そのあとに分身の術で2人増える。
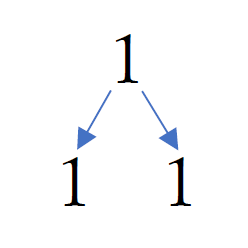
こんな感じ。
そして増えた二人がまた分身の術をする。
この時、ぶつかった人たちは足し算されて「2」に進化する。
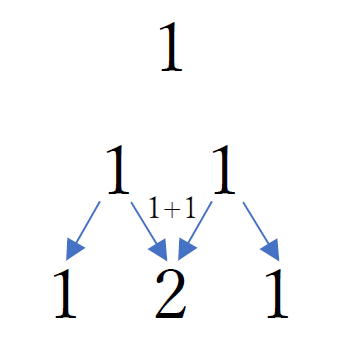
こんな感じ。
この分身の術とぶつかって進化を繰り返していくと、三角形ができる。
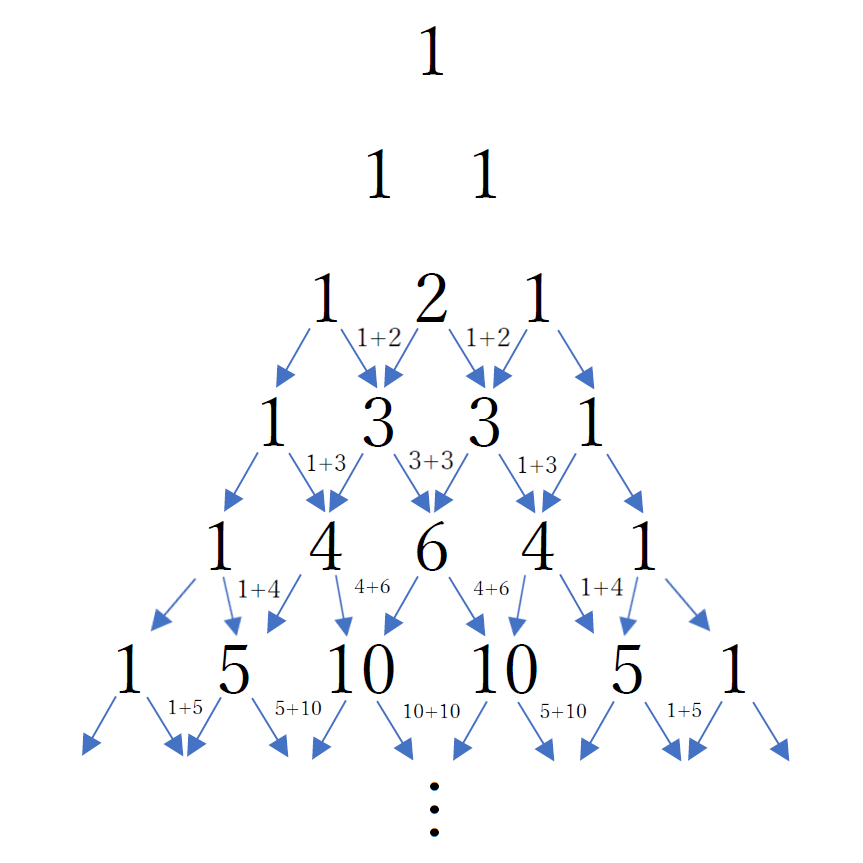
こんな感じ。
これがパスカルの三角形の作り方。
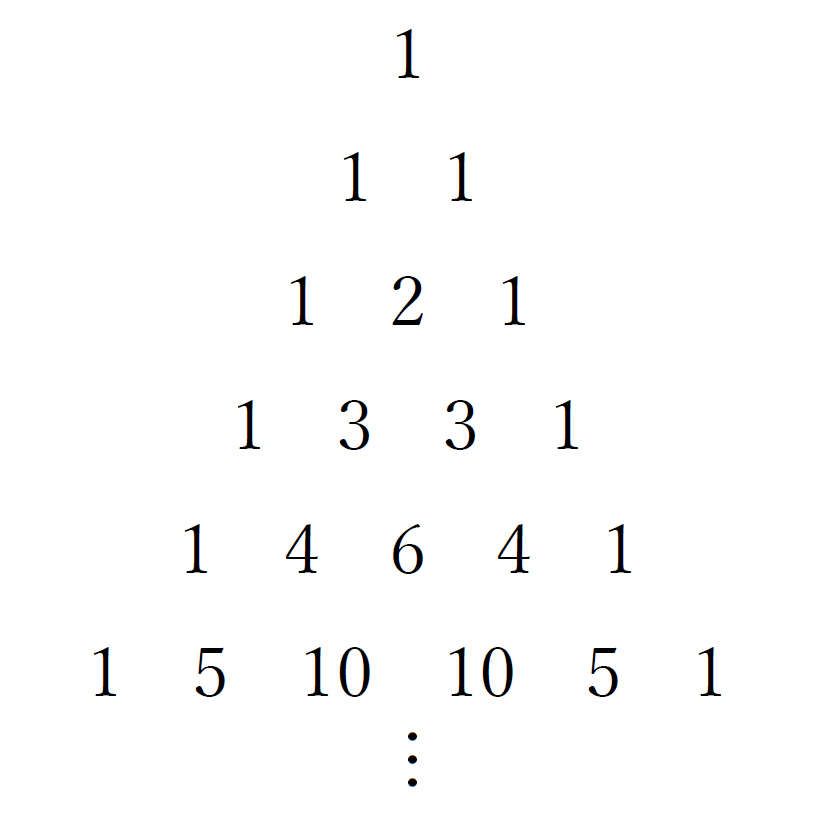
じゃあこの三角形は何に使えるのか。
使いどころは、二項展開の公式。
二項展開っていうのは
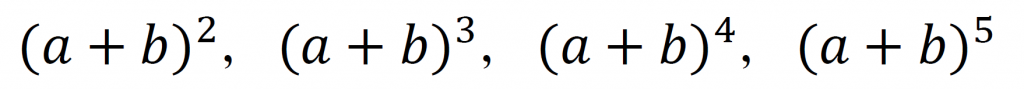
こーゆー人たち。
じゃあ、どうやって使うのか。
0乗と1乗も含め、まず、この人たちを展開してみると、
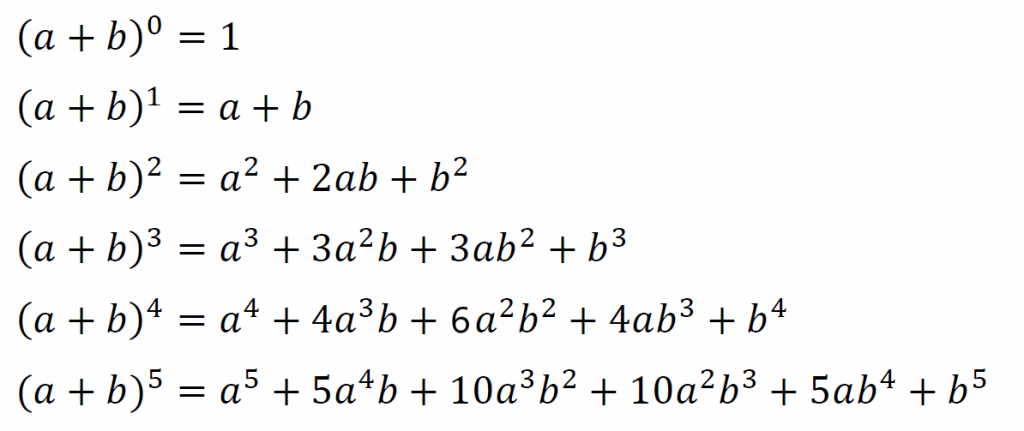
こんな感じになる。
ここで、それぞれの係数と、あらかじめ用意しておいたパスカルの三角形と見比べてみる。
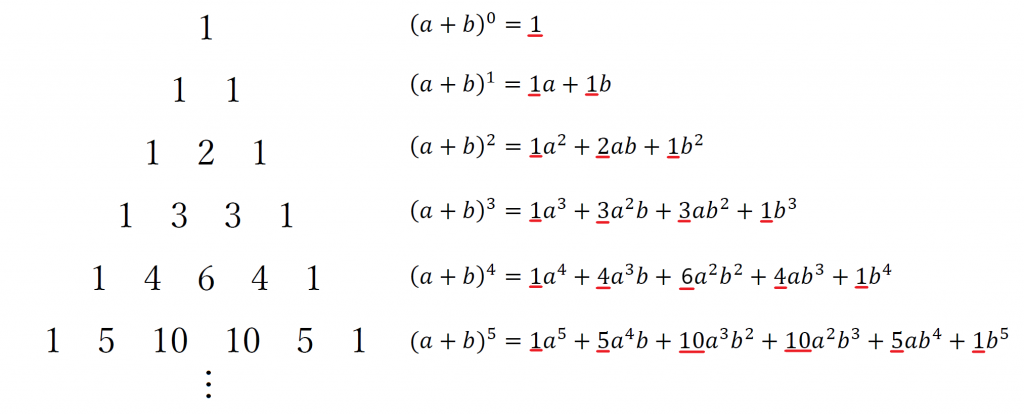
係数は単項式において、その数の部分。
こんな感じにパスカルの三角形のそれぞれの段が展開の公式の係数部分に対応しているのが分かる。
それぞれの展開の公式で係数が何かを考えるときにパスカルの三角形を使う。
これがパスカルの三角形の使い方。
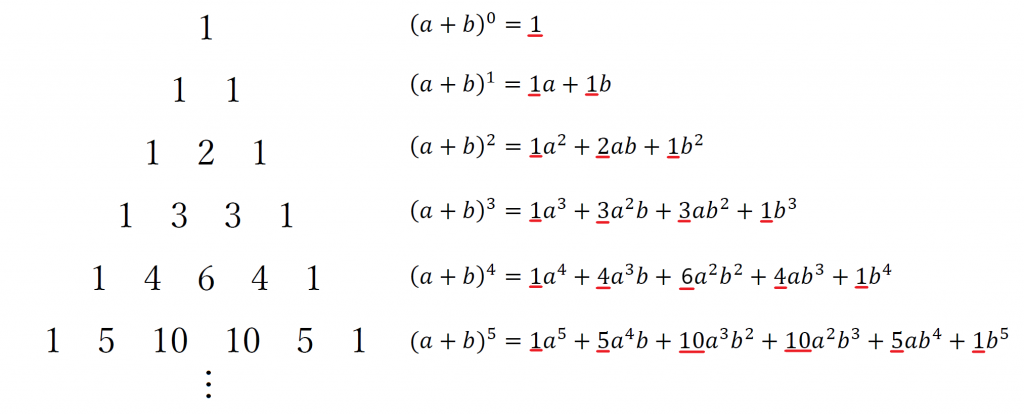
展開の公式の係数部分は分かった。
でも二つの文字の指数はパスカルの三角形では表されていない。
指数部分がどういう数字になるのか。
これも覚え方がある。
もう一度それぞれの展開の公式を見てみる。
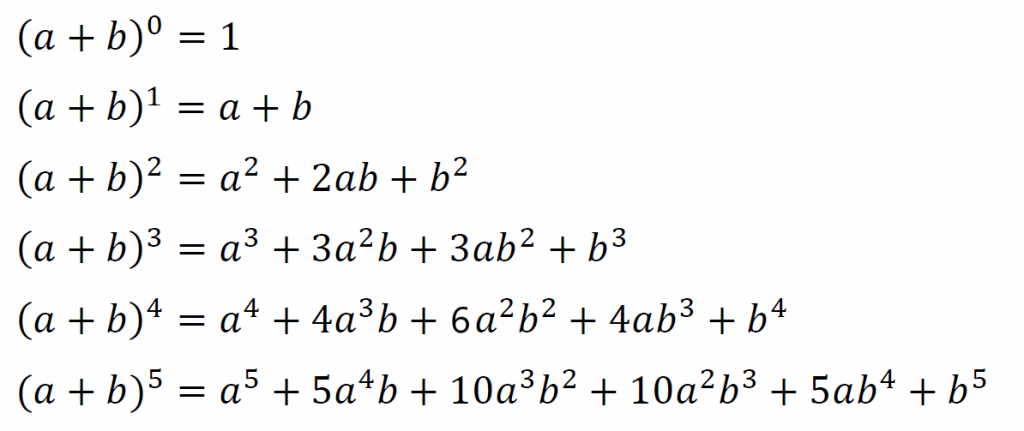
この中で一番大きい5乗の展開の公式を見てみると、
まず、aに注目。
そしてaの指数に注目。
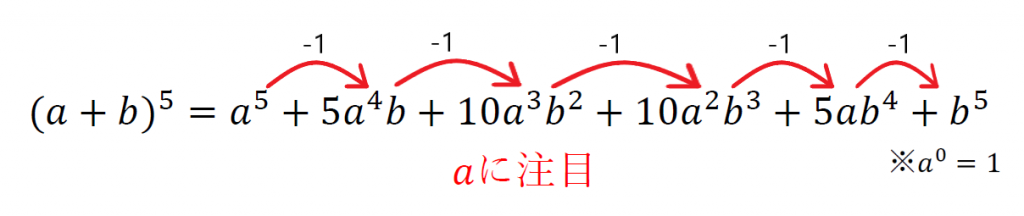
先頭にaの5乗が来ている。
そこから右に行くにつれて4,3,2と指数が一つずつ減っている。
これでaの指数部分の法則が分かった。
次にbに注目。
そしてbの指数に注目。
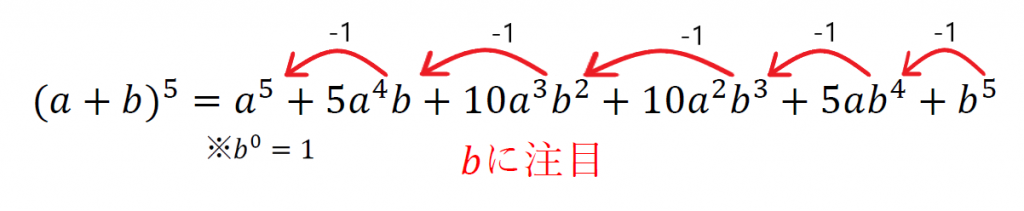
最後尾にbの5乗が来ている。
そこから左に行くにつれて4,3,2と指数が一つずつ減っている。
これでbの指数部分の法則も分かった。
もう一度それぞれの展開の公式を並べて見てみる。
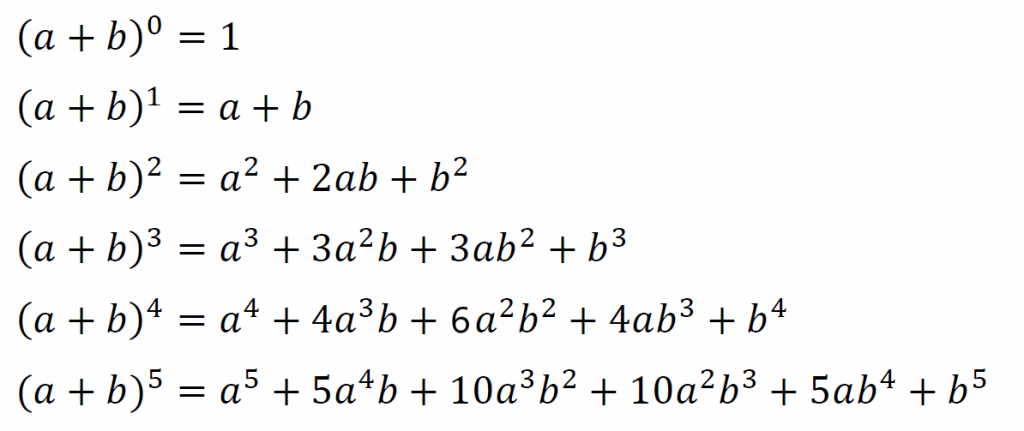
どの累乗の式も同じような法則で指数が書かれていることが分かる。
注意しなくてはならないのが、最初と最後は文字が一種類だけということ。
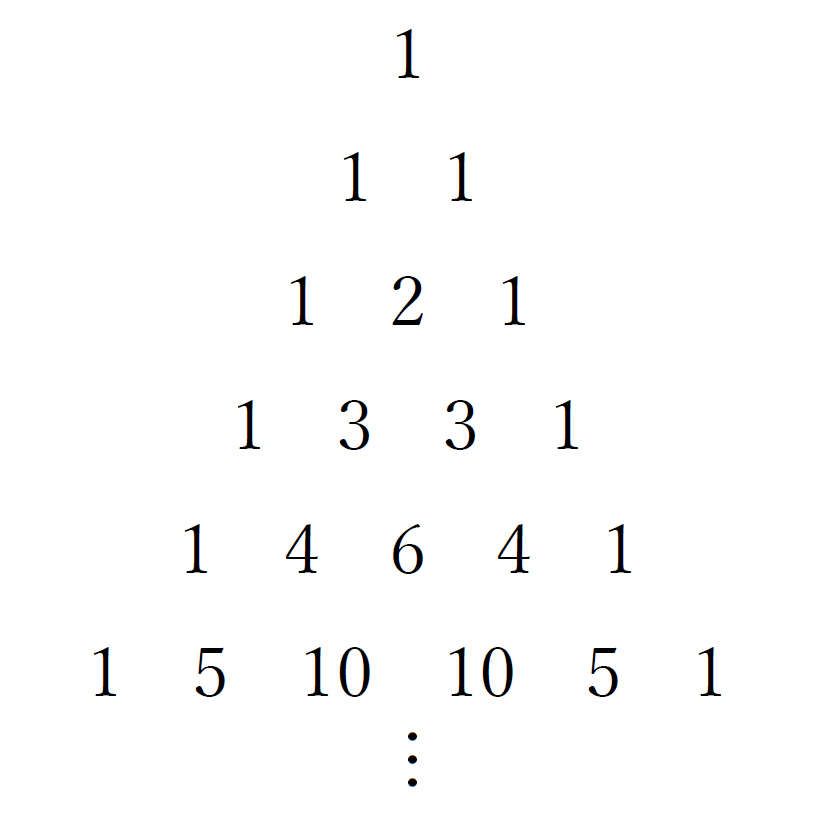
これが「パスカルの三角形」。
仕組みを理解するのと同時に、定義を知っておくことも大事。
| パスカル | ブレーズ・パスカルさん |
| パスカルの三角形 | 二項展開における係数を三角形状に並べたもの(Wikipediaより) |
| 係数 | 単項式において、その数の部分。 |
| 指数 | 数や文字の右肩に付記して、その累乗を示す数字や文字 |
| 累乗 | 同じ数を順次に掛け合わせること。 |
二項展開
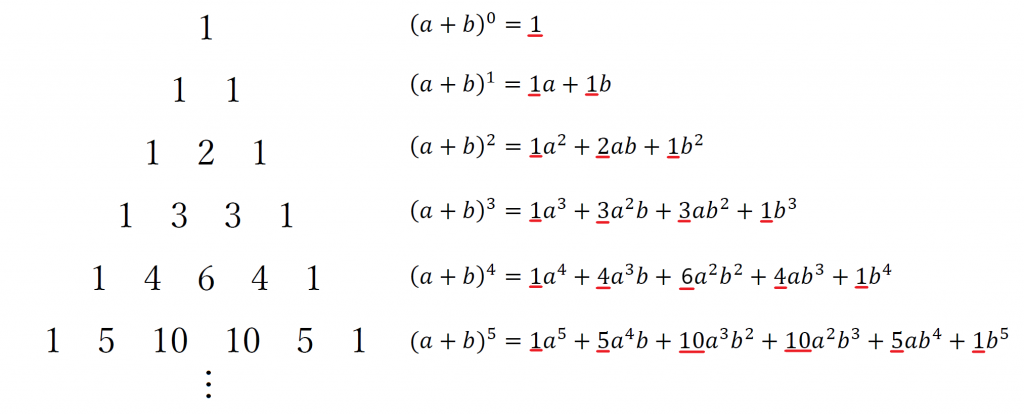
範囲で見ると数学Ⅱの範囲らしいけど、こういった小技を覚えておくと問題を素早く解くことができると思う。
3乗以降の展開の公式は、「パスカルの三角形」で覚える方がおヌヌヌ。
要は、係数が何の数字になるかを示してくれる道具みたいなもの。
分からなくなったらその場で余白にパスカルの三角形を書いてみよう。
結構使える。
 すうがくのいえ
すうがくのいえ