対称式とは、文字を入れ替えても、元の式と同じ式になる式のこと。

こういうのが対称式。
文字が3つの場合も、対称式と呼ぶ。

こんな感じ。

文字が3つの基本対称式がこの3つ。
文字が2つの基本対称式が2つなのに対して、文字が3つの基本対称式は3つある。
文字が2つの対称式の性質として、
「どんな対称式も、2つの基本対称式の足し算、引き算、掛け算の組み合わせで表すことができる」
ということが知られている。
文字が3つの対称式の場合も同じ感じで、
「どんな対称式も、3つの基本対称式の足し算、引き算、掛け算の組み合わせで表すことができる」
という性質を持っている。
本当に文字が3つの対称式も、3つの基本対称式の足し算、引き算、掛け算の組み合わせで表すことができるのか、
2次の対称式の場合と、3次の対称式の場合とで分けて確認してみる。

まずは、2次の対称式から考えてみる。
3文字2次式の因数分解の公式により、
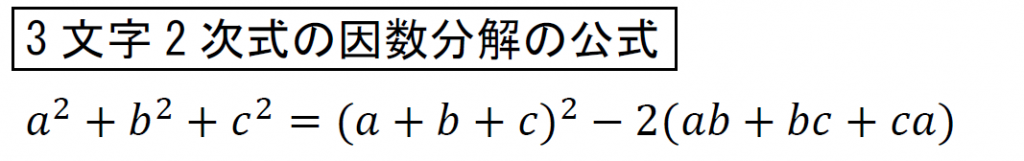
それぞれ、xとyとzで考える。
ここで、基本対称式が使われているのかを見てみると、

こんな感じに、基本対称式のみで表すことができている。
これが文字が3つの2次の対称式を基本対称式で表す場合。

次は3次の対称式を考えてみる。
この式は結構出てくるので基本対称式に直せるようになっておきたい。
3文字3次式の因数分解より、
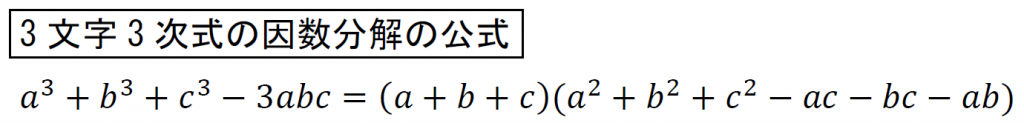
それぞれ、xとyとzで考える。

これで基本対称式のみで表すことができた。
これが文字が3つの3次の対称式を基本対称式で表す場合である。

文字が3つの対称式の場合は、基本対称式が3つある。
3文字2次式の因数分解と3文字3次式の因数分解の公式も合わせて覚えておきたい。
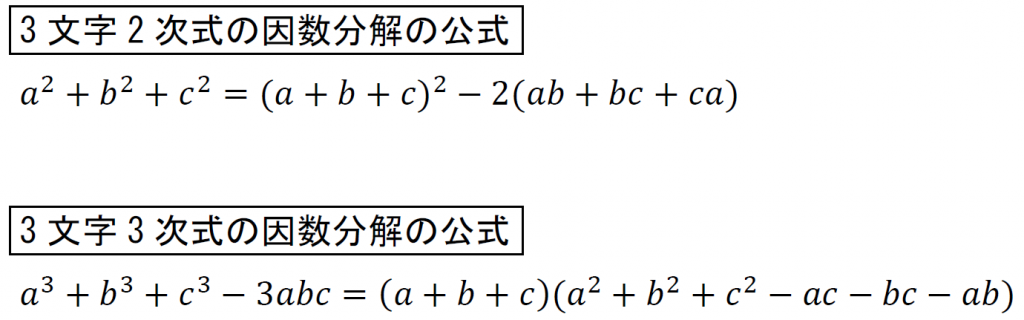
対称式とは、文字を入れ替えても、元の式と同じ式になる式のこと。
文字が2つの対称式の性質として、
「どんな対称式も、2つの基本対称式の足し算、引き算、掛け算の組み合わせで表すことができる」
文字が3つの対称式の場合も同じ感じで、
「どんな対称式も、3つの基本対称式の足し算、引き算、掛け算の組み合わせで表すことができる」
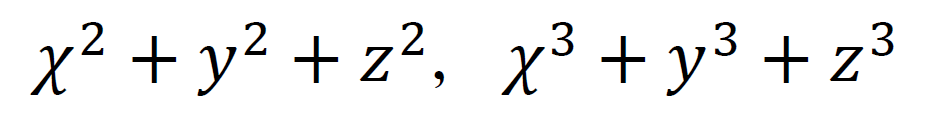
文字が2つの基本対称式が2つなのに対して、文字が3つの基本対称式は3つある。
文字の個数が変われば基本対称式の数も変わるということは覚えておきたい。
基本対称式の使い方が分かれば、
対称式を変形させて比較的簡単に対称式を基本対称式のみで表すことができる。
そのためにも、対称式かどうかを判断できるようになっておくべき。
それも、問題の数をこなせば自然と見えてくるようになる。
 すうがくのいえ
すうがくのいえ