見栄え。
一言で言うと見栄え。
規則性があって美しさを求めたとき、「輪環の順(りんかんのじゅん)」を使う。
逆に、規則性も美しさも求めないのであれば、 「輪環の順」 は関係のないお話。
なので、「輪環の順」を求められていない限り、試験とかで減点されることはない。
本当に予備知識的な位置。
目次

とりあえず「輪環の順」っていうのはこんなイメージ。
a,b,cの3つのアルファベットの場合、
a→b → c → a → b → c → a → …
という感じに、
循環することを意識した式の書き方
これが「輪環の順」。
「輪環の順」は、循環することを意識した式の書き方ということが分かった。
じゃあ実際に輪環の順で書ける式はどんな式なのかを見ていこう。

例えばこの式を展開したとき、

こんな感じの答えになった。
これでも正解。
これを「輪環の順」に並べると、

こんな感じになる。
これでも正解。
aからアルファベット順に並び、規則性があって美しいとされている式の形。
他にも、

この式を因数分解したとき、

こんな感じの答えになった。
これでも正解。
これを「輪環の順」に並べると、

こんな感じになる。
これでも正解。
aからアルファベット順に並び、規則性があって美しいとされている式の形。

回るイメージの図を覚えておけば十分。
一応言葉での定義も知っておけば更に十分。
| 輪環の順 (りんかんのじゅん) | a→b→c→a→…という、 循環することを意識した式の書き方 |

「輪環の順」は、あくまで式の書き方のお話。
「規則性があって美しいとされている式の形」の式の書き方のお話。
式の見栄えのお話。
特に輪環の順を求めている問題でなければ、これができないからと言って問題を解くことに支障はない。
といいつつも、輪環の順を使う方が良いという事もある。
長い計算をする途中式で、規則性を持たせたキレイな形にしておくことで、計算をした自分にとっても見やすくなる。
自分にとっても見やすい形ということは、そこから計算ミスが起こることを減らすことができる。
計算ミスは、急いで書いたせいで文字が崩れていたり、途中式を飛ばして暗算で解くときとかによく起こる。
式自体に規則性を持たせることができるところで、輪環の順に並び替えておくことで、式のどこに何があるのかということが瞬時に分かる。
もっと言うと、式自体を見なくてもどういう式なのかということを頭の中で考えることさえできる。
規則性のある式を想定して、計算ミスを減らすことは知っておいても損はないんじゃないかと思う。
ただ、
必須ではない。
 すうがくのいえ
すうがくのいえ 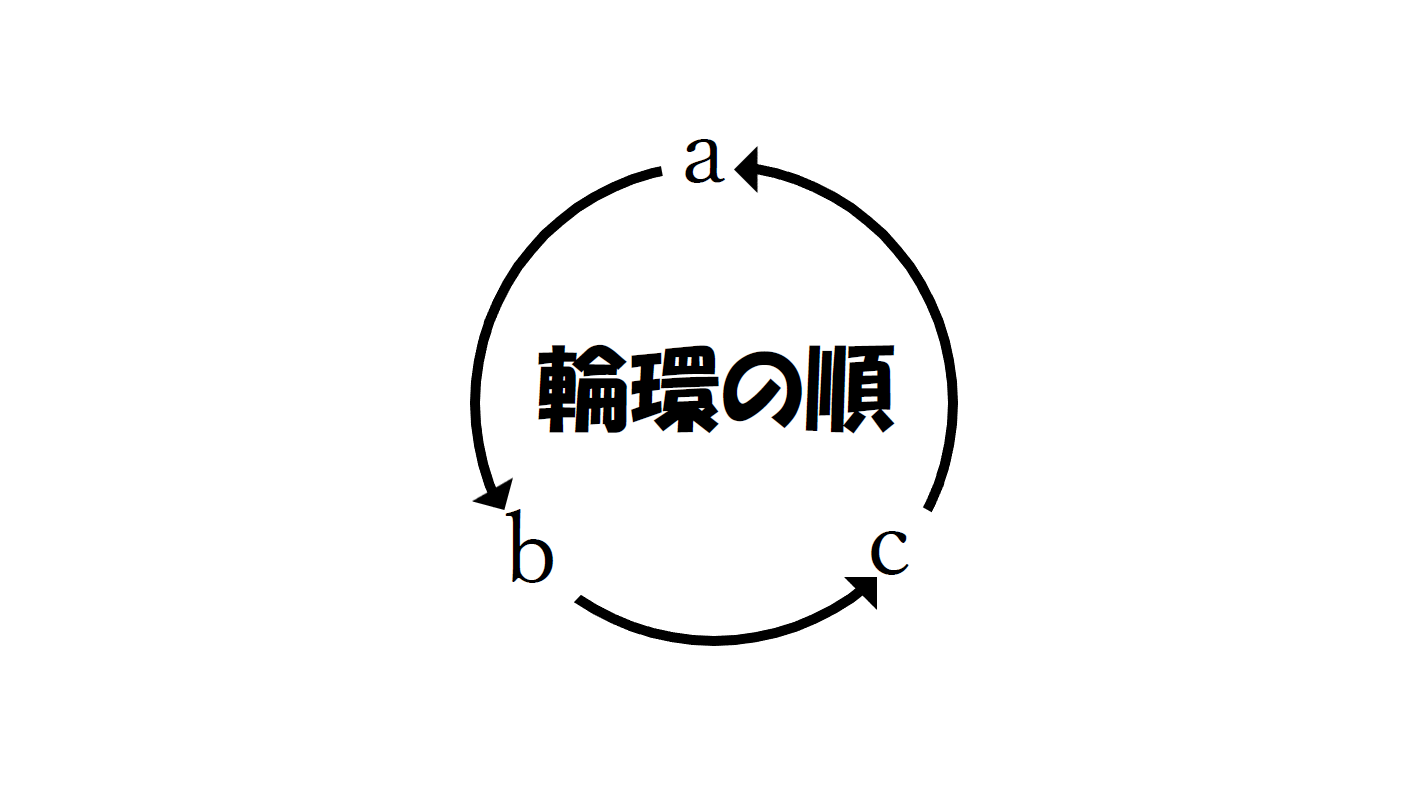


≪…「規則性があって美しいとされている式の形」…≫から、フィボナッチの
≪…「輪環の順」…≫のような記事を見つける。
≪…車輪の中心にある「空」…≫を、□とする数の言葉ヒフミヨ(1234)の自然数について、解析接続としての
[ フィボナッチ数列の「総和」が -1 になる ]は、円環運動と線分の往復運動との風景として観る。
円環の線分(直径)の[-1][0][+1]にフィボナッチ数列(0 1 1 2 3 5 8 ・・・)を円環運動の方向を線分に割り当てると、
[-1] [0] [+1] 運動の向き
1 1 0 ←
2 3 →
8 5 ←
とすると、中心から円環への直線運動は、
1×0 - 1² = -1
円環から中心への直線運動は、
2×1 - 1² = +1
中心から円環への直線運動は、
3×1 - 2² = -1
・・・ ・・・
となる。この風景は、自然数を創り出していくコトが[-1]と観える・・・
円環の中心の回転点が□になると夢想したい・・・
ながしかく□でまとめ〇になる
数学的洞察と哲学的考察は、抽象概念を具体的な「風景」として捉える示唆に富む試みです。
直径上の運動モデル([-1, 0, +1])から生じる-1と+1の交互のパターンは、「『自然数を創り出す』行為が、この運動では『-1』として現れる」と解釈されます。この象徴的な「-1」は、フィボナッチ数列の通常の意味での総和は有限の値を持ちませんが、解析接続という手法によってその「総和」が「-1」と見なされる数学的事実と呼応しています。
「ながしかく□でまとめ〇になる」という言葉は、この思想を集約します。「円環の中心の回転点が□になる」という夢想は、中心[0]が単なる点ではなく、起源や容器としての「空」(□)の性質を持つことを示唆します。そして、「ながしかく□でまとめ〇になる」とは、線形的・離散的な要素(□)が、根底にある円環運動という全体的文脈(〇)の中で統合され、一つの完全な理解(〇)に至る様を表現しています。
つまり、個々の断片的な動き(□)が循環する全体のシステム(〇)の中で捉えられた時、解析接続によってフィボナッチ数列の「総和」と見なされる「-1」という値が、深遠な真理として美しい哲学的洞察と共に立ち現れる、というご考察と受け取りました。