基本的な分母の有理化

分数の式の中で、分母にルートを含む式が出てくることがある。
そんなときは、「分母の有理化」をすることで、式を簡単にすることができる。
つまり、
分母の有理化とは、分母にルートがない形に変形させること。
「有理化」の意味は、簡単に言うとルートを外すという意味。
分母の有理化をする前提として、展開の公式２．を知らなくてはならない。

こーゆーやつ。
分母の有理化で使うときは、それぞれにルートを付けて考える。

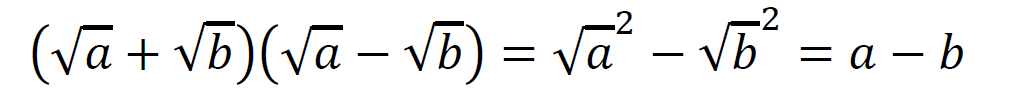
こんな感じになる。
2乗の形にすることでルートを外す（有理化する）ことができる。

それを踏まえ、分母の有理化をするために、

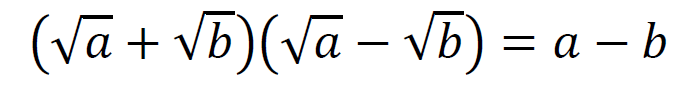
この式を大量に使う。
在庫が無くならないように気を付けて。

分母の有理化の原理

分母の有理化は大きく分けて2種類ある。
何はともあれ、とりあえず分母の有理化を一旦やってみよう。

１．

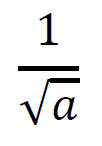
１つ目は、分母にルートがある状態の分数を想定する。
分母にルートがあるので、ここから分母にルートがない状態に有理化させていく。

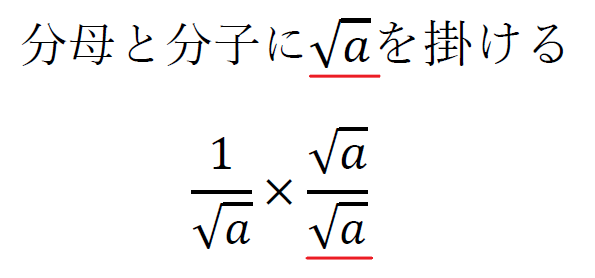
こんな感じに分子と分母に同じものを掛ける。
そのまま計算すると、

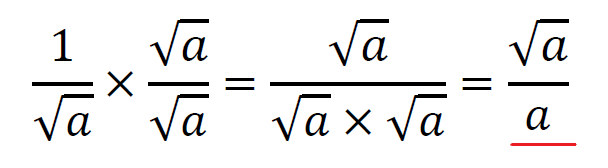
こんな感じに分母にルートがなくなった。
これで1つ目の分母の有理化ができた。

２．

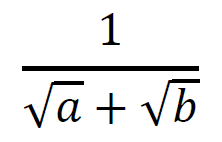
2つ目は、分母にルートを含む「式」がある分数を想定する。
分母にルートがあるので、ここから分母にルートがない状態に有理化させていく。

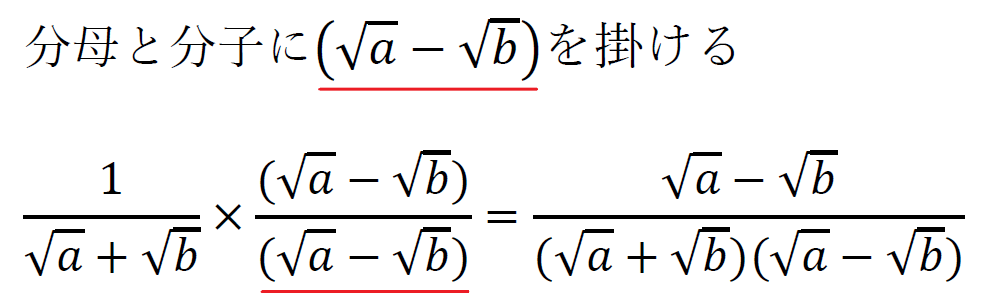
こんな感じに、分母と分子に「分母の式の符号を変えた式」を掛ける。
ここで、最初に確認した展開の公式２．のルートを付けたバージョンを使う。

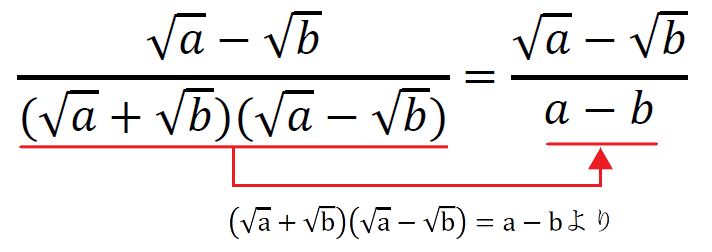
こんな感じに分母にルートがなくなった。
これで2つ目の分母の有理化ができた。

この2種類の分母の有理化を主に使っていくのでしっかり覚えておきたい。
2つ目は少し慣れが必要になると思うから、最初は途中式を省略せずにゆっくり解いていけば計算ミスも減る。

定義を知る

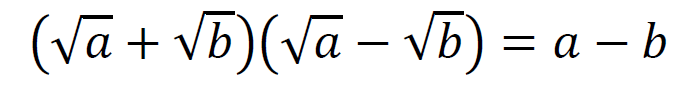
この式を元に分母を有理化していく。

まとめ

分数の式の中で、分母にルートを含む式が出てきたとき、
「分母の有理化」をすることで、式を簡単にすることができる。
ルートの扱いに慣れれば、分母の有理化はそんなに難しくない。
基本ができなければ、応用はできない。
逆に言えば、基本さえしっかりしていれば、いくらでも応用できる。

なぜ「分母の有理化」をした方が良いのかについては、
「キレイな形だ」とか「計算しやすいから」とかがよく言われている。
個人的には、
その理由として、本来分母に来る数は有理数が多いからなのではないかと思う。
有理数が来ることが多いというだけで、無理数が来るということもある。
なので、どっちかというと、
分母に来ることが多い有理数にしておいた方がいいんじゃね？って感じなんじゃないかと思う。
なので分母の有理化という作業があり、
その作業で分数を統一することで「キレイな形だ」とか「計算しやすいから」ということに繋がるのではないかと思う。