すうがくのいえ 
符号というのは、正（プラス）か負（マイナス）のどちらか。
つまり、2つの数を比べたときプラスとマイナスの状態を異符号という。
符号が同じ場合は同符号っていう。
符号が一定であることを表す「定符号」というのがあるけど、それはまた別のお話。
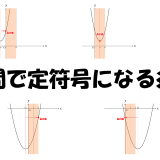【2次不等式】区間で定符号になる条件
実数\(p,q\)の大小関係が\(p\)＜\(q\)のとき、\(f(x)=ax^2+bx+c(a≠0)\)について\(f(p)\)と\(f(q)\)が異符号ならば、2次方程式\(f(x)=0\)は\(p\)＜\(x\)＜\(q\)の間に必ず実数解を1つもつという性質が成り立つ。
こんな感じ。長いので一つずつ分けると、
１．実数\(p,q\)の大小関係が\(p\)＜\(q\)のとき
２．\(f(x)=ax^2+bx+c(a≠0)\)について\(f(p)\)と\(f(q)\)が異符号ならば
３．2次方程式\(f(x)=0\)は\(p\)＜\(x\)＜\(q\)の間に必ず実数解を1つもつ
という性質が成り立つので、グラフを交えながら順番に見ていく。
１．実数\(p,q\)の大小関係が\(p\)＜\(q\)のとき
これはそのまま、2つの実数の大小関係を表す。
𝑥に\(p\)を代入すると\(f(p)\)、𝑥に\(q\)を代入すると\(f(q)\)となる。
代入した結果\(f(p)\)と\(f(q)\)の符号を比べたとき、
・\(f(p)\)はプラス、\(f(q)\)はマイナス
・\(f(p)\)はマイナス、\(f(q)\)はプラス
こんな感じに\(f(p)\)と\(f(q)\)がプラスとマイナスであれば「異符号」となる。
・\(f(p)\)はマイナス、\(f(q)\)はプラス
つまり、「\(f(p)\)と\(f(q)\)が異符号」というのは
３．2次方程式\(f(x)=0\)は\(p\)＜\(x\)＜\(q\)の間に必ず実数解を1つもつ
2次方程式\(f(x)=0\)は\(ax^2+bx+c=0\)のこと。
\(ax^2+bx+c=0\)の実数解が\(p\)と\(q\)の間に必ず１つあることを表す。
2次関数\(f(x)=ax^2+bx+c\)で考えると、必ず𝑥軸と交わるということ。
・\(a\)＞\(0\)のとき
・\(a\)＜\(0\)のとき
「\(f(p)\)＞\(0,f(q)\)＜\(0\)」のときも「\(f(p)\)＜\(0,f(q)\)＞\(0\)」のときも、2点\((p,f(p)),(q,f(q))\)を結ぶ連続した曲線は、区間\(p\)＜\(x\)＜\(q\)の間で\(f(x)=0\)を満たす点、つまり𝑥軸と交わる点をもつ。
なので、2次方程式\(f(x)=0\)は区間\(p\)＜\(x\)＜\(q\)の間に必ず実数解を1つもつことが分かる。
こんな感じに、連続な関数がある区間で定義され、区間の両端の関数値が異符号であるとき、その区間内に関数値が0になる点が少なくとも1つ存在することを中間値の定理という。
ここでは関数値が\(0\)になる点に注目したけど、関数値が\(0\)以外の任意の値に対しても同様に成り立つ。
以上から
実数\(p,q\)の大小関係が\(p\)＜\(q\)のとき、\(f(x)=ax^2+bx+c(a≠0)\)について\(f(p)\)と\(f(q)\)が異符号ならば、2次方程式\(f(x)=0\)は\(p\)＜\(x\)＜\(q\)の間に必ず実数解を1つもつという性質が成り立つ。
ということが分かる。
少し簡単にすると、
\(f(x)=ax^2+bx+c(a≠0)\)について
\(p\)＜\(q,f(p)･f(q)\)＜\(0\:\:\:\)のとき\(\:\:\:p\)＜\(x\)＜\(q\)の間に\(f(x)=0\)の実数解を必ず1つもつ
こんな感じ。
\(p\)＜\(q,f(p)･f(q)\)＜\(0\:\:\:\)のとき\(\:\:\:p\)＜\(x\)＜\(q\)の間に\(f(x)=0\)の実数解を必ず1つもつ
同符号は、「プラスとプラス」か「マイナスとマイナス」。
なので
下に凸\((a\)＞\(0)\)の場合で考えてみると、
なので、同符号（\(f(p)･f(q)\)＞\(0\)）だと実数解をもつかどうか判断できない。
・区間①\(0\)＜\(x\)＜\(2\)
・区間②\(3\)＜\(x\)＜\(5\)
実際に\(f(x)=0\)を因数分解して解を求めてみると、
区間①\(0\)＜\(x\)＜\(2\)と区間②\(3\)＜\(x\)＜\(5\)の中に実数解があるということが分かる。
グラフで見てみると
こんな感じ。
| 異なる符号ということ | |
| 同じ符号ということ | |
| 符号が一定ということ | |
| 連続な関数がある区間で定義され、区間の両端の関数値が異符号であるとき、その区間内に関数値が0になる点が少なくとも1つ存在する。関数値が0以外の任意の値に対しても同様に成り立つ。 |
関数の値が、ある区間で異符号をとる場合、その区間内に実数解が存在する。
これは、連続な関数がある値をはさんで符号が変化するとき、その間に値をとる点があるという性質（中間値の定理）から分かる。
一方、関数が同符号をとる場合には、符号の変化がない以上、𝑥軸と交差する（＝解がある）とは限らない。
こんな感じに、関数の符号に注目することで、2次方程式の解の存在範囲を把握できる。
2次方程式の性質を考えるときには、「異符号」という視点を一つのツールとして活用していきたい。
