解の存在範囲から考える𝑥軸との共有点の位置

ある区間で関数の値が異符号なら、その間に必ず解があるという性質から、2次関数のグラフが𝑥軸とどこで交わるのかが判断できる。
つまり「解の存在範囲」から𝑥軸との共有点の位置が分かる。
この共有点を\(α,β(α\)≦\(β)\)とおき、任意の実数\(k\)が\(α,β\)の「外側」にあるか「内側」にあるかで、関数の値の符号や軸の位置まで決定できる。式からグラフと𝑥軸との関係を読み解く力が大事。

合わせて読みたい

異符号ってなに？2次方程式の解の存在範囲

𝑥軸との共有点の位置
- １．2つの解の外側
- ２．2つの解の内側
どんな問題で役立つ？
例題
- （１）
- （２）
定義を知る
まとめ

𝑥軸との共有点の位置

2次関数\(f(x)=ax^2+bx+c(a\)＞\(0)\)のグラフと𝑥軸が交わる点の𝑥座標を\(α,β(α\)≦\(β)\)とすると、任意の実数\(k\)が次のどちらに位置するかによって\(f(k)\)の符号が変わる。
また、判別式や軸の位置からも、グラフの位置を確定させることができる。

１．2つの解の外側

「任意の実数\(k\)の位置が2つの解の外側のとき」というのは「\(k\)＜\(α\)≦\(β\)」か「\(α\)≦\(β\)＜\(k\)」のときを指す。
このとき、関数の値\(f(k)\)は正の値をとる（\(f(k)\)＞\(0\)）。
また、𝑥軸と交わるので判別式\(D\)は\(0\)以上（\(D\)≧\(0\)）で、\(k\)＜\(α\)≦\(β\)なら軸は\(k\)より右（軸＞\(k\)）、\(α\)≦\(β\)＜\(k\)なら軸は\(k\)より左（軸＜\(k\)）となる。
まとめると、
・\(k\)＜\(α\)≦\(β\)　のとき　\(f(k)\)＞\(0\)、\(D\)≧\(0\)、軸＞\(k\)
・\(α\)≦\(β\)＜\(k\)　のとき　\(f(k)\)＞\(0\)、\(D\)≧\(0\)、軸＜\(k\)
というのが導き出せる。

２．2つの解の内側

「任意の実数\(k\)の位置が2つの解の内側のとき」というのは「\(α\)＜\(k\)＜\(β\)」のときを指す。
このとき、関数の値\(f(k)\)は負の値をとる（\(f(k)\)＜\(0\)）。
外側のときと違って、下に凸の放物線で\(f(k)\)＜\(0\)ならば必ず𝑥軸と異なる2点で交わるので、判別式は必ず\(D\)＜\(0\)となる。
また、別途軸の位置を検討する必要もない。
まとめると、
・\(α\)＜\(k\)＜\(β\)　のとき　\(f(k)\)＜\(0\)
というのが導き出せる。

任意の実数\(k\)が2つの解の外側か内側かで
・\(k\)＜\(α\)≦\(β\)　のとき　\(f(k)\)＞\(0\)、\(D\)≧\(0\)、軸＞\(k\)
・\(α\)≦\(β\)＜\(k\)　のとき　\(f(k)\)＞\(0\)、\(D\)≧\(0\)、軸＜\(k\)
・\(α\)＜\(k\)＜\(β\)　のとき　\(f(k)\)＜\(0\)
となる性質を使い分けることができるようになりたい。
今見たのは下に凸の放物線のお話。
上に凸(\(a\)＜\(0\))のときは
・\(k\)＜\(α\)≦\(β\)　のとき　\(f(k)\)＜\(0\)、\(D\)≧\(0\)、軸＞\(k\)
・\(α\)≦\(β\)＜\(k\)　のとき　\(f(k)\)＜\(0\)、\(D\)≧\(0\)、軸＜\(k\)
・\(α\)＜\(k\)＜\(β\)　のとき　\(f(k)\)＞\(0\)
こんな感じに、\(f(k)\)の符号が異なる。
また、状況によっては「＜」が「≦」になったり「≧」が「＞」になったりと符号の種類が変わるので、問題文をよく読んで解いていきたい。

どんな問題で役立つ？

例えば2次関数で、 \[y=x^2-mx+m^2-3m\] が𝑥軸の正の部分において異なる2点で交わるとき、\(m\)の範囲はどうなるのか考えてみる。
𝑥軸の正の部分において異なる2点で交わるというのは、\(y=f(x)\)のグラフが𝑥軸の\(x\)＞\(0\)の部分と異なる2点で交わるということ。
なので、共有点の𝑥座標を\(α,β(α\)＜\(β)\)とすると、\(0\)＜\(α\)＜\(β\)となることが分かる。
ここで、さっきの任意の実数を\(k=0\)と考えると、
・\(0\)＜\(α\)＜\(β\)　のとき　\(f(0)\)＞\(0\)、\(D\)＞\(0\)、軸＞\(0\)
という性質を使うことができる。

\(f(x)=x^2-mx+m^2-3m\)から

判別式\(D=b^2-4ac\)から

\(y=x^2-mx+m^2-3m\)から

①\(m\)＜\(0,3\)＜\(m\)かつ②\(0\)＜\(m\)＜\(4\)かつ③\(m\)＞\(0\)を数直線で見ると

こんな感じ。
よって \(3\)＜\(m\)＜\(4\) これが答え。
今度は𝑥軸の正と負の部分で交わるとき、\(m\)の範囲はどうなるのか考えてみる。
𝑥軸の正と負の部分で交わるというのは、\(y=f(x)\)のグラフと𝑥軸が異なる2点で交わり、その交点の𝑥座標のうち一方が\(0\)より大きくもう一方が\(0\)より小さいということ。
なので、共有点の𝑥座標を\(α,β(α\)＜\(β)\)とすると、\(α\)＜\(0\)＜\(β\)となることが分かる。
同じように、任意の実数\(k=0\)と考えると、
・\(α\)＜\(0\)＜\(β\)　のとき　\(f(0)\)＜\(0\)
という性質を使うことができる。

さっき求めた\(f(0)=m^2-3m\)から\(f(0)\)＜\(0\)より

よって \(0\)＜\(m\)＜\(3\) これが答え。
グラフの形とか位置をイメージすることが大事。

例題

例題を解きながら、𝑥軸との共有点の位置の性質を確認していく。

（１）

\(f(x)=x^2+2x+a\)とおいて考える。
「\(1\)より大きい解と\(1\)より小さい解を1つずつもつ」というのは、\(f(x)=x^2+2x+a\)のグラフと𝑥軸が異なる2点で交わり、その交点の𝑥座標のうち一方が\(1\)より大きくもう一方が\(1\)より小さいということ。
なので、共有点の𝑥座標を\(α,β(α\)＜\(β)\)とすると、\(α\)＜\(1\)＜\(β\)となることが分かり、
・\(α\)＜\(1\)＜\(β\)　のとき　\(f(1)\)＜\(0\)
という性質を使うことができる。

\(f(x)=x^2+2x+a\)から

よって \(a\)＜\(-3\) これが答え。

（２）

\(f(x)=x^2-2kx+3k\)とおいて考える。
「\(2\)以上の異なる2つの実数解をもつ」というのは、\(f(x)=x^2-2kx+3k\)のグラフが𝑥軸の\(x\)≧\(2\)の部分と異なる2点で交わるということ。
なので、共有点の𝑥座標を\(α,β(α\)＜\(β)\)とすると、\(2\)≦\(α\)＜\(β\)となることが分かり、
・\(2\)≦\(α\)＜\(β\)　のとき　\(f(2)\)≧\(0\)、\(D\)＞\(0\)、軸＞\(2\)
という性質を使うことができる。

\(f(x)=x^2-2kx+3k\)から

判別式\(D=b^2-4ac\)から

\(y=x^2-2kx+3k\)から

①\(k\)≦\(4\)かつ②\(k\)＜\(0,3\)＜\(k\)かつ③\(k\)＞\(2\)を数直線で見ると

こんな感じ。
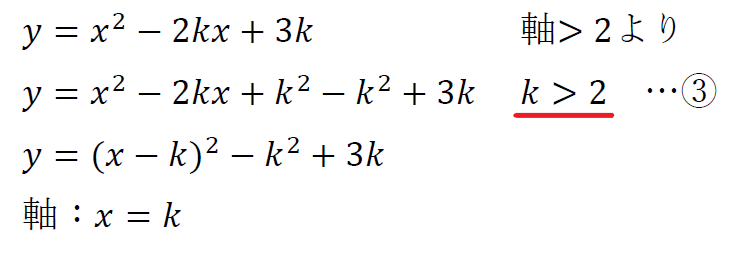
よって \(3\)＜\(k\)≦\(4\) これが答え。

定義を知る

2次方程式	\(ax^2+bx+c=0\) （\(a,b,c\)は定数、\(a≠0\)）
2次関数	\(y=ax^2+bx+c\) （\(a,b,c\)は定数、\(a≠0\)）
\(f(x)\)	\(y\)が\(x\)の関数であること表すときに、「\(y=f(x)\)」と書くことができる

まとめ

2次関数と𝑥軸との共有点の位置について、解の存在範囲をもとにグラフの位置がどうなるのかを整理してみた。
任意の実数\(k\)が2つの解の外側か内側かで
・\(k\)＜\(α\)≦\(β\)　のとき　\(f(k)\)＞\(0\)、\(D\)≧\(0\)、軸＞\(k\)
・\(α\)≦\(β\)＜\(k\)　のとき　\(f(k)\)＞\(0\)、\(D\)≧\(0\)、軸＜\(k\)
・\(α\)＜\(k\)＜\(β\)　のとき　\(f(k)\)＜\(0\)
となる性質を使い分けることができるようになりたい。
グラフの形とか位置をイメージすることが大事。