多項式の整理とは、同類項をまとめて整理するということ。
「同類項をまとめる作業」
と
「整理する作業」
に分けて考えていく。

「同類項をまとめる作業」はこんな感じ。
「同類項」を「まとめる」ということ。そのまま。
ある意味これはもう整理された姿なのかもしれないけど、
「整理する作業」は同類項をまとめる作業とは別にある。
「降べきの順に整理」と「昇べきの順に整理」の2種類。

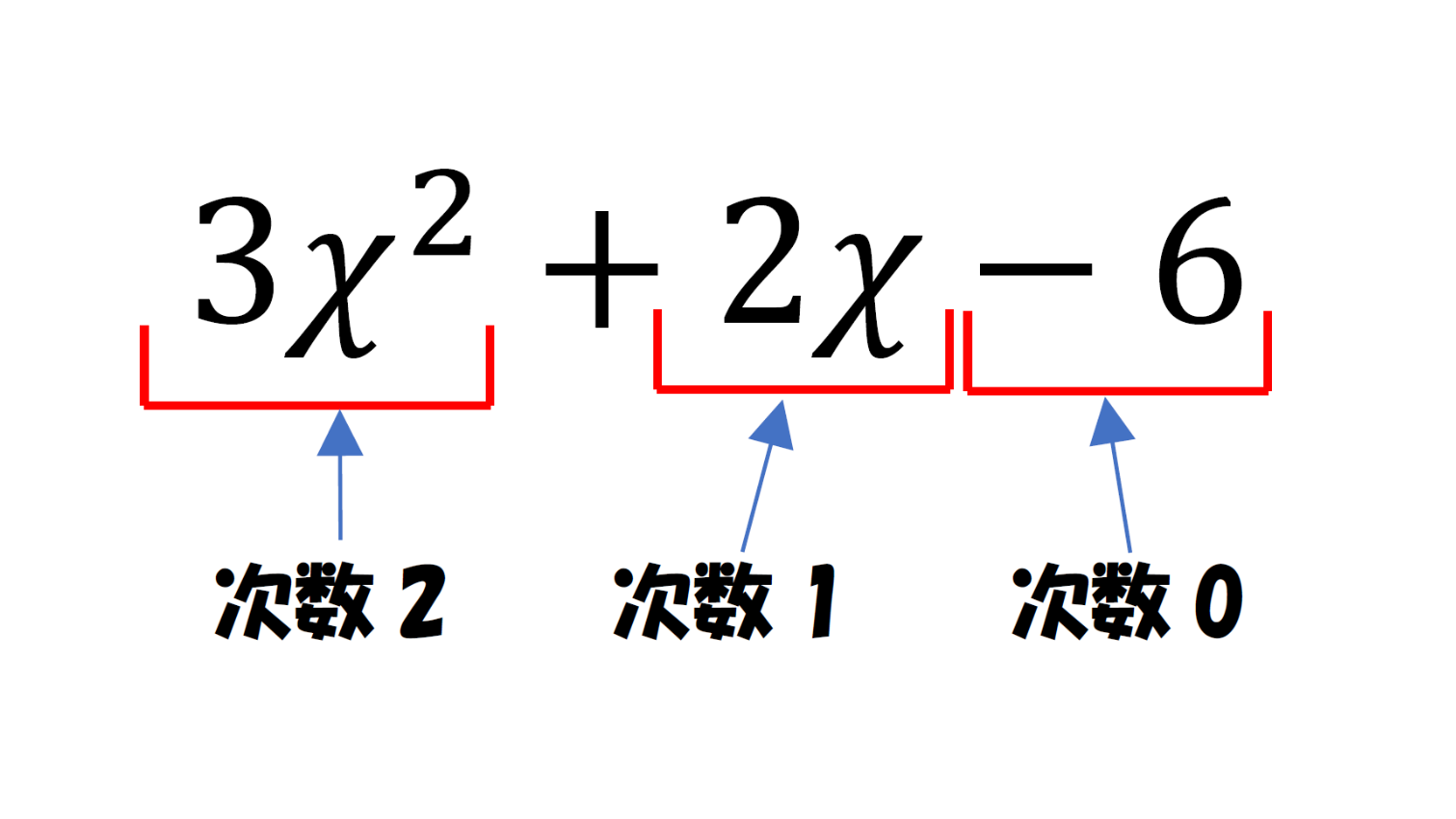
「降べきの順に整理」は、こんな感じ。
項の次数の高い方から順に並べるということ。
高いところから低いところへ降りていくイメージ。
よく使う。

「昇べきの順に整理」は、こんな感じ。
項の次数の低い方から順に並べるということ。
低いところから高いところへ昇っていくイメージ。
あまり使わない。

2種類以上の文字を持つ単項式の「ある特定の文字に着目」する。
つまり「\(x\)」とか「\(y\)」とか「\(x\)と\(y\)の両方」とかに着目するということ。
着目するっていうのは、他の文字や数字を単なる数として見るということ。
そうすると、同じ単項式でも着目の仕方によって次数や係数が変わる。
次数は、掛け合わせた文字の個数(文字の指数の和) のこと。
係数は、単項式において、その数の部分のこと。
同類項がまとまっていないとか、多項式の整理ができてない状態だと、バラバラな状態で単項式の特定の文字に注目することがちょっと難しい。
だから、同類項をまとめて整理された多項式である必要がある。
その上で、特定の文字に着目して、着目した文字以外の文字や数字を単なる数として見る。

この単項式の「\(x\)について着目」すると、

次数は2。
次に、「\(y\)について着目」すると、

次数は1。
今度は、「\(x\)と\(y\)について着目」すると、

こんな感じの扱いになる。
次数は3。
今回の場合、どの文字に着目するかで次数も係数も全然違うということが分かる。

| 降べきの順に整理 | 項の次数の高い方から順に並べること 高いところから低いところへ降りていくイメージ |
| 昇べきの順に整理 | 項の次数の低い方から順に並べること 低いところから高いところへ昇っていくイメージ |
| 特定の文字に着目 | ・2種類以上の文字を含む単項式において、着目する 文字によって、式の次数、係数が変わる。 ・着目する文字は一つとは限らない。 ・着目した文字以外の文字は単なる数と考える。 |

特定の文字に着目すると、 着目した文字以外の文字や数字を単なる数として見るということになる。
そして、着目する文字によって、次数や係数は変わる。
同じ場合もある。
し、違う場合もある。
 すうがくのいえ
すうがくのいえ