どれだけ公式を覚えても、
どれだけ技を磨いても、
あらかじめ知っていないと、
初見では進めないだろってヤツがいる。
どうしても突破できない問題がある。
解いてみて出した答えが間違えていた、とかではなく、
そもそも答えまでたどり着けない
それでもどうにかして突破したいが、
解ける気がしないお手上げ状態になった問題。
余力がある人は、まず問題だけを見て解いてみてほしい。

この式を因数分解する。
3乗がある時点でもうそっとペンを置きたくなる。
しかも文字が3つ。
どこから手を付ければいいのか分からない。
とりあえず展開して「aについて降べきの順に整理」する。

3乗の係数である(b-c)と形を合わせるために、
aの係数は-1でくくり、
定数項は共通因数bcでくくる。

ここで、aの係数と定数項が何やらいじれそう。
因数分解の公式を使って分解していくと、
(b-c)が共通因数でくくることができるようになる。

ここからペンが1ミリも進まなくなった。
どう頑張ってもaの3乗が邪魔すぎて因数分解できなかった。
これは知っておかなければ多分解けないと思う。
次にやることは、{ }の中を展開する。
ここに来て展開はヤバい。

そろそろ何やってるのか分からなくなる頃。
展開してどうするのかというと、
「bについて降べきの順に整理」する。
これはもう分からん。

aで整理してたところ、急にbで整理し始めるのは知らないと無理。
整理すると、{ }の中で(c-a)が共通因数になりそうなことが分かるから、
それに向けて因数分解していく。

ここまでくると、(c-a)が見えてくるから、くくっちゃう。

あとは、{ }の中が因数分解できそうだから、

こんな感じになって、一応終わり。
これでも正解。
正解なんだけど、欲を言うとキレイに整理したいから、「輪環の順」を使っちゃう。

綺麗な形にしたらこんな式になる。
これでも正解。
これで因数分解できた。
| 輪環の順 (りんかんのじゅん) | a→b→c→a→…という、 循環することを意識した式の書き方 |
| 降べきの順に整理 | 項の次数の高い方から順に並べること 高いところから低いところへ降りていくイメージ |
| 昇べきの順に整理 | 項の次数の低い方から順に並べること 低いところから高いところへ昇っていくイメージ |
| 特定の文字に着目 | ・2種類以上の文字を含む単項式において、着目する 文字によって、式の次数、係数が変わる。 ・着目する文字は一つとは限らない。 ・着目した文字以外の文字は単なる数と考える。 |
知っておかなければならないわけではないが、知っておくと問題を解きやすくなる。
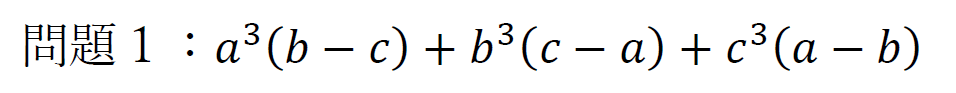
解き方が分かった上でもう一度何も見ずに解いてみると結構身に付く。
解いた結果が間違えていたとかではなく、
そもそも答えまでたどり着けない問題にぶち当たることというのは何度もあると思う。
個人的に、それはとても良いことだと思う。
自分の持ち合わせてる武器に何が足りてないのかを知ることができるから。
解ききって間違えるよりも、得られるものが多い気がする。
何が足りてないか気付いたときは結構すっきりする。
気がする。
牛丼食べたい。
 すうがくのいえ
すうがくのいえ .png)

.png)