平方式と完全平方式と平方完成が何なのかは分かった。
次は、その平方式の作り方というのを確認していく。
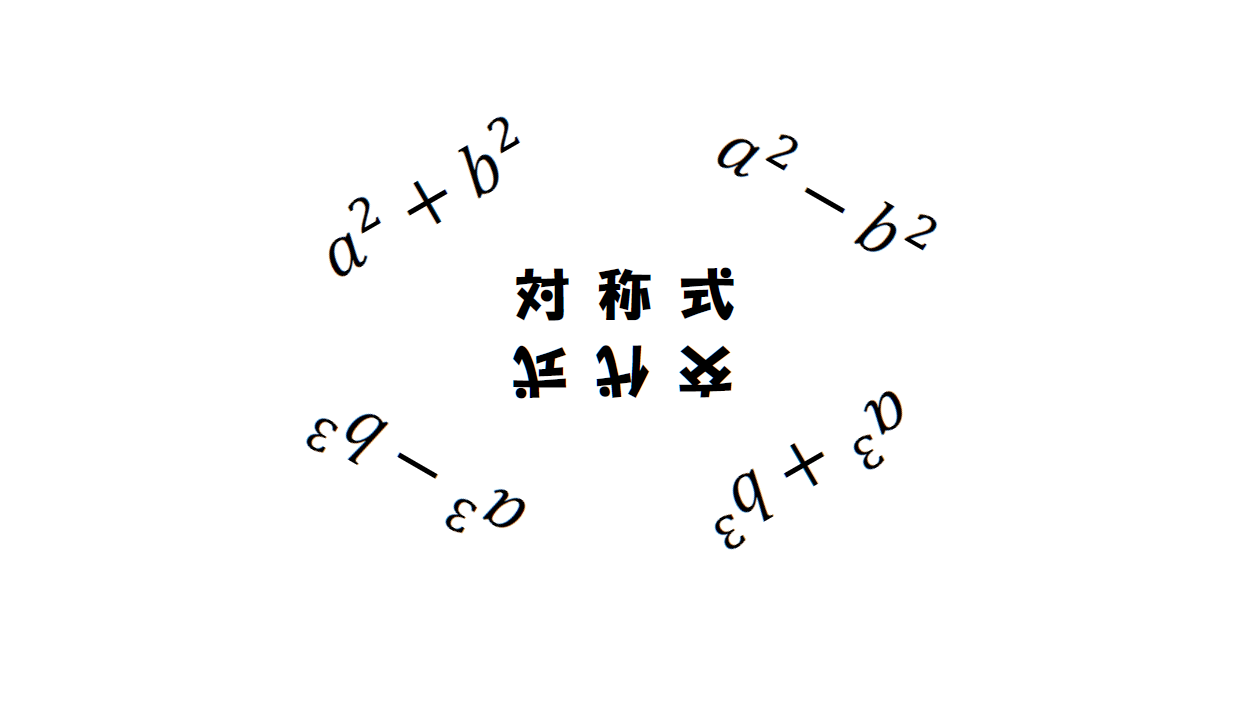
平方式というのは、
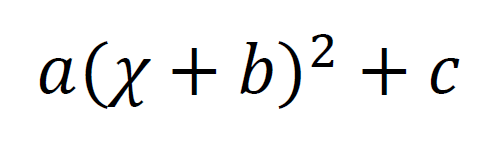
こういう感じの式。
今からこんな感じの平方式を作る。

まず、こんな感じに、2乗のペアの式を作る。
ここから、

こんな感じに、プラスとマイナスの2種類の平方式を作ることができる。
1つずつ確認していこう。

まずはプラスの方。

こうんな感じに式を変形することができる。
式を整理すると、

となるので、因数分解の公式1.を使って、

こんな感じに因数分解できる。
ここから、加えたものを除く。

つまり、式で書くと、

( )外すと、

これで平方式の形になった。

プラスはこんな感じ。

次にマイナスの方。

こうんな感じに式を変形することができる。
式を整理すると、

となるので、因数分解の公式1.を使って、

こんな感じに因数分解できる。
ここから、加えたものを除く。

つまり、式で書くと、

( )外すと、

これで平方式の形になった。

マイナスはこんな感じ。

こんな感じ。
プラスとマイナスの2種類の平方式を作ることができるということに注意。

じゃあ具体的にどうやって因数分解で使うのかを、具体的な問題で考えてみる。
今回の問題は、平方式を作ることで因数分解をすることができる。
4乗…
4乗て。
と、ちょっと距離を置きたくなるような式。
でもここで、「16は4の2乗」というところに注目。
少し式を入れ替えると、

ここで!
平方式に変形!

を使って、少し計算すると、

といった感じで、因数分解ができるプラスの方の平方式に変形させればいいことが分かる。

同類項をまとめると、

こんな感じになる。
ここでまた因数分解の公式を使いたいところだけど、ややこしいから分かりやすくするために置き換えて計算を進める。

ここで因数分解の公式2.を使って、

ここまで因数分解して、置き換えた文字を元の形に戻す。

これで一応因数分解できた。
これでも正解。
すこし整理すると、

これが割ときれいな形。
これでも正解。
どっちでも正解。
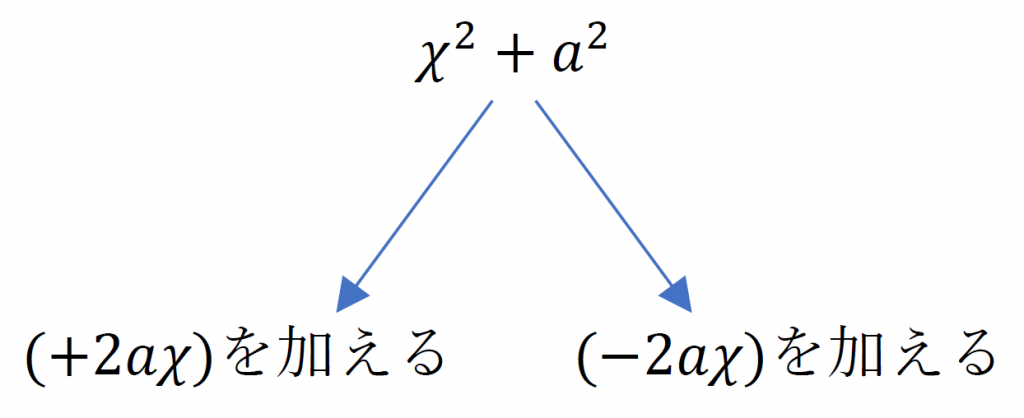
2乗のペアの式を作ることができれば、平方式を2種類作ることができるということに注意。

| 平方 | ある数を2乗すること |
| 平方完成 | 二次の多項式を平方式や完全平方式に変形させること |

平方式に変形させて因数分解して解く問題は、問題自体に結構特徴がある。
似たような問題を解いて、平方完成をすることに慣れておけば、
グラフを書くとき、式を変形させることが苦じゃなくなる。
「二次関数のグラフ」で役立ちますように。
 すうがくのいえ
すうがくのいえ