平方根の公式

2乗するとaになる数を、「aの平方根」って言い方をする。
そんな平方根にも公式が３つある。
公式というより、法則という方がしっくりくるかもしれない。

とりあえず、どんな公式なのかを見てみる。

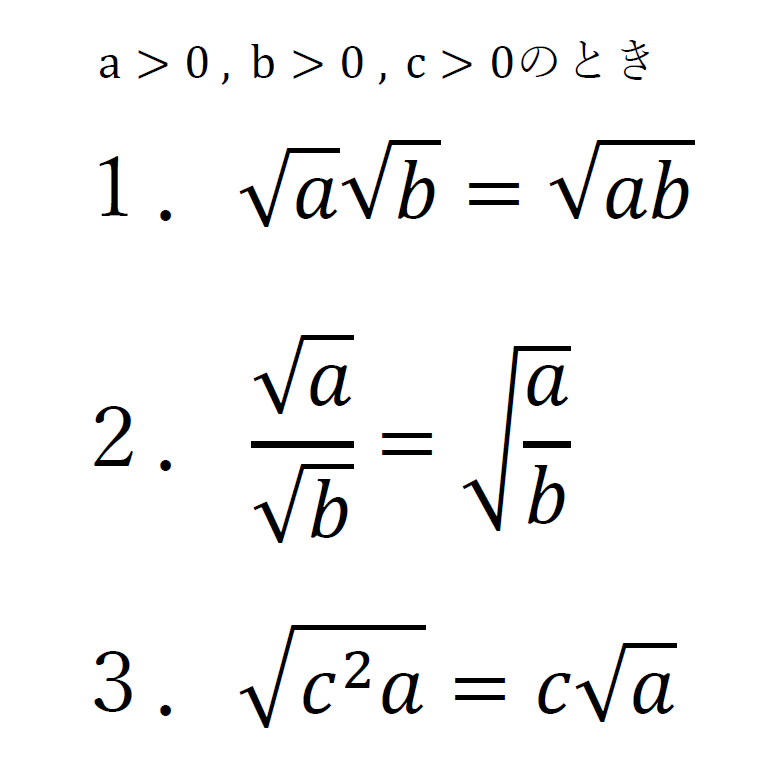
この３つ。
とりあえずは、これさえ覚えておけば、ルートの計算は大体できると思う。
使い方は問題を解きまくって覚えていけば良き。
1つずつ見ていこう。

１．

「平方根×平方根はどうなるんですか～」っていう式。
まず左辺の式を2乗し、指数法則３．を使う。

2乗するとaになる数が、「aの平方根」なので、2乗するとルートが外れる。
ルートが外れた結果、「ab」になった。
「ab」は右辺のルートの中身と同じであることが分かる。
ここで、もう一度左辺の式に注目する。

実数の範囲だと、ルートの中身は必ずプラスになる。
2乗するとaになる数を、「aの平方根」っていうので、

ということができる。
これが１つ目の公式。
めちゃくちゃ簡単に言うと、

こんな感じ。
実際に数字を入れて、公式を使うと、

という感じの使い方ができる。
これで公式１．が導き出せた。

２．

「平方根の分数はどうなるんですか～」っていう式。
これもさっきと同じように、まず左辺の式を2乗し、指数法則３．を使う。

2乗するとaになる数が、「aの平方根」なので、2乗するとルートが外れる。
ルートが外れた結果、「a/b」になった。
「a/b」は右辺のルートの中身と同じであることが分かる。
ここで、もう一度左辺の式に注目する。

実数の範囲だと、ルートの中身は必ずプラスになる。
2乗するとaになる数を、「aの平方根」っていうので、

ということができる。
これが２つ目の公式。
めちゃくちゃ簡単に言うと、

こんな感じ。
実際に数字を入れて、公式を使うと、

という感じの使い方ができる。
これで公式２．が導き出せた。

３．

ルートの中に2乗となる数字や文字があったときのお話。
平方根の公式１．を左辺で使うと、

ここで、cに注目すると、正の数の平方根と分かるから、

こんな感じにルートを外すことができる。
これが３つ目の公式。
実際に数字を入れて、公式を使うと、

という感じの使い方ができる。
これで公式３．が導き出せた。

定義を知る

とりあえず、この３つを覚えておけばルートの計算は大体できる。

まとめ

平方根の公式を知っておけば、
これから出てくるルートに関する問題にも応用できる。
そのためにも、やっぱり基礎が一番大事。
基礎を固めるためにたくさん問題を解いて身につけなければならない。
ルートとお友達になれれば、いろんな角度から問題を見ることができるようになる。
いろんな角度から問題を見ることができるようになれば、問題を楽しく解くことができるようになる。