ルートを整数部分と小数部分に分けて計算するとき、数直線をイメージすると分かりやすい。
とりあえず、プラス方向の「ルート」を考える。

数直線上のルートの配置がこんな感じ。
なんか最後の方すごく密になってる…。
この密具合も、なんとなく見ておけばイメージの手助けになる。
ルート(平方根)っていうのは、2乗するとルートの中の数になる数のこと。

ルートにはそれぞれ整数部分と小数部分がある。
ルート=【整数部分】+【小数部分】
こんな感じでルートは構成されている。
「ルートの整数部分」と「ルートの小数部分」を順番に判断していこう。

例えば、これらの数の【整数部分】と【小数部分】が何かを考える。
もう一度数直線を見てみると、

こんな感じの位置にいらっしゃる。
ここで、何の整数の間にいるかを考えなくてはならない。
このとき、いきなり何の整数の間にいるかを考えるんじゃなくて、
整数になるルートが何なのかをまず考えてから整数に直す。
どういうことかというと、

こんな感じに、整数になるルートというのは限られているから、それを踏まえてそれぞれのルートの位置を考える。
ルートの位置を整数と整数の間に確定することができたら、
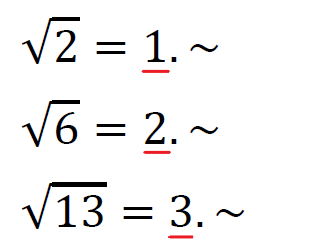
こんな感じに整数部分がどういう値になるのかが分かる。
これで、まず【整数部分】を求めることができた。

次は【小数部分】を考える。
小数部分は、ルートから整数部分を引くと出てくる。
つまり、小数部分はルートと整数部分の引き算の式で表すことになる。
これで、【小数部分】も求めることができた。
整数部分と小数部分を求めることで、
ルート=【整数部分】+【小数部分】
で表すことができる。

具体的に整数部分と小数部分の値が求められている例題を見てみる。
とりあえず分母にルートがあるから、分母の有理化をする。

こんな感じに、分母を有理化した分数の形になる。
ここから、ルート=【整数部分】+【小数部分】で表すことを考える。
まずは、√2の【整数部分】が何かを考える。

こんな感じに小数で表すと「1.~」となるので、整数部分が「1」になるということが分かる。
これで、まず【整数部分】を求めることができた。
次に、【小数部分】が何かを考える。
分母の有理化を済ませた例題の数を見てみると、分母が「2」の分数であることが確認できる。
分母が「2」ということは、分子が2の倍数にならないと整数にならないということ。

分子が「2+√2」、つまり、分子が「2+1.~」だと、数直線上では、
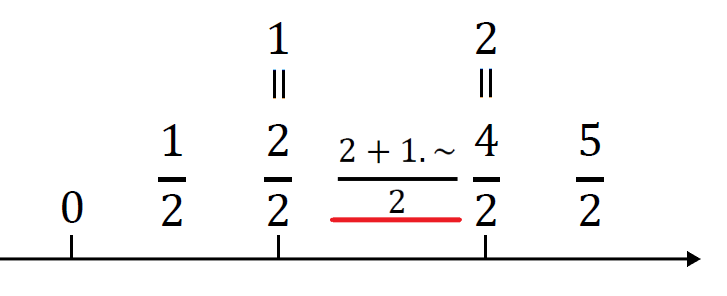
こんな感じの位置関係になる。
なので、

という風に考えなくてはならない。
これで【整数部分】を求めることができた。
次に、【小数部分】が何かを考える。
小数部分は、ルートと整数部分の引き算の式で表すことになる。

これで、【小数部分】も求めることができた。

ルートの構成
ルート=【整数部分】+【小数部分】

まずは【整数部分】、「何の整数の間にいるか」を考える。
それから【小数部分】、「整数部分を引く」。
分数のときは分母の倍数が分子になる時が整数部分になる。
 すうがくのいえ
すうがくのいえ 

