今度は、複2次式の4次関数の最大・最小を考える。

例えば\[y=x^4+4x^3+3x^2-2x-6\]こんな感じの関数のこと。
4次式とは、最も次数の高い項の次数が「4」の式ということ。
関数とは、数の関係性のこと。
2つの変数\(x,y\)において、\(x\)が決まることで\(y\)が決まるとき、\(y\)は\(x\)の関数であるという。
これが4次関数。
4次関数の正体が分かったので、4次関数の最大・最小を考えていく。
☆複2次式
\(x^4\)と\(x^2\)と定数項のみからなる4次式を複2次式と呼ぶ。「\(x^4\)」とか「\(x^4+2x^2\)」とか「\(x^4-4x^2+4\)」とかとか。複2次式は\(x^2=t\)と置くことで「\(x^4=t^2\)」とか「\(x^4+2x^2=t^2+2t\)」とか「\(x^4-4x^2+4=t^2-4t+4\)」という感じに「\(t\)の2次式」とすることができる。4次関数の最大・最小は微分法を使う数学Ⅲの範囲だけど、複2次式であれば数学Ⅰの範囲でも解くことができる。
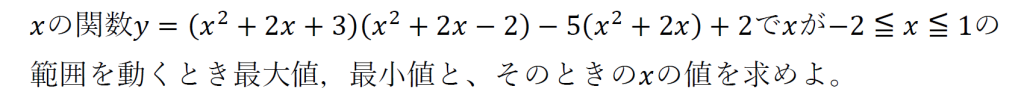
と思いきや\((x^2+2x+3)(x^2+2x-2)\)を展開すると\(x^4\)が出てくるということが分かる。
でも解き方としてはそのまま展開したりはしない。
1.共通の式を置き換え
まずは\((x^2+2x+3)(x^2+2x-2)-5(x^2+2x)+2\)で\(x^2+2x\)という式が共通していることを見つける。
\(x^2+2x=t\)と置き換える。
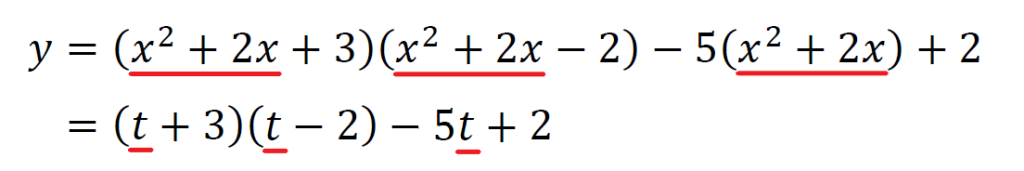
2.変域の確定
置き換えてまずやることは、\(t\)の変域を確定させること。
そのためにはまず平方式に平方完成する。
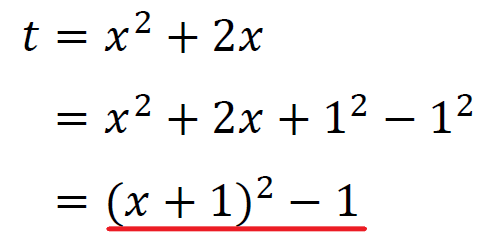
ここで2次関数の最大値と最小値の考え方を取り入れる。
所与の条件より\(-2≦x≦1\)であることから
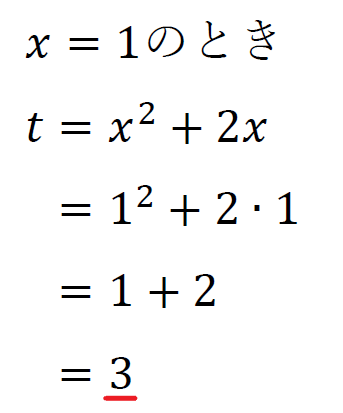
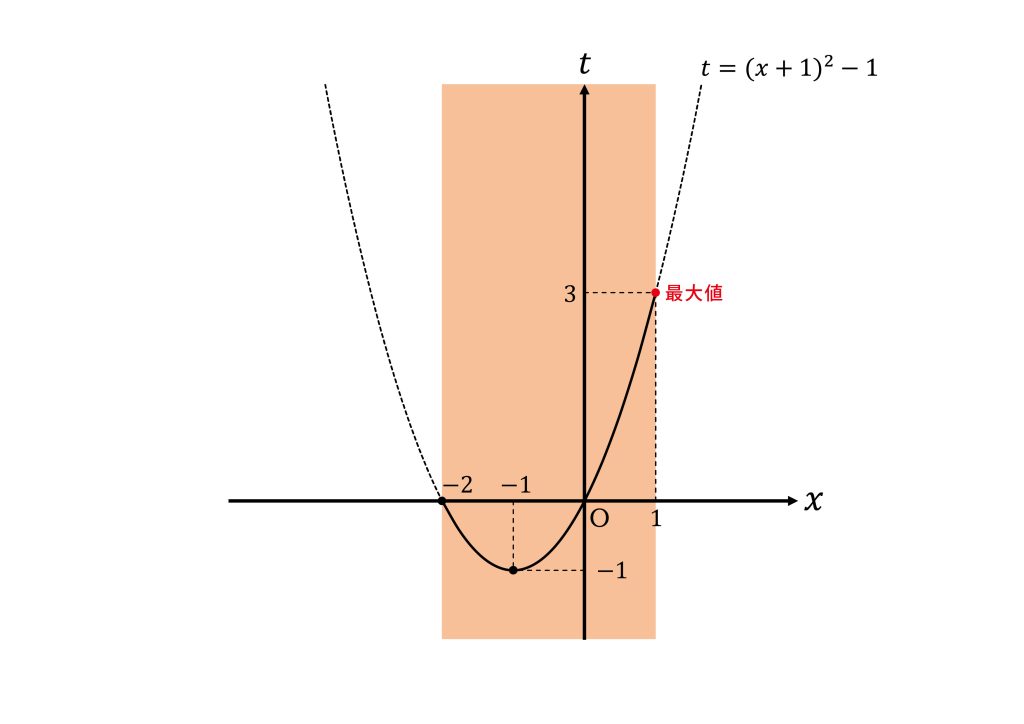
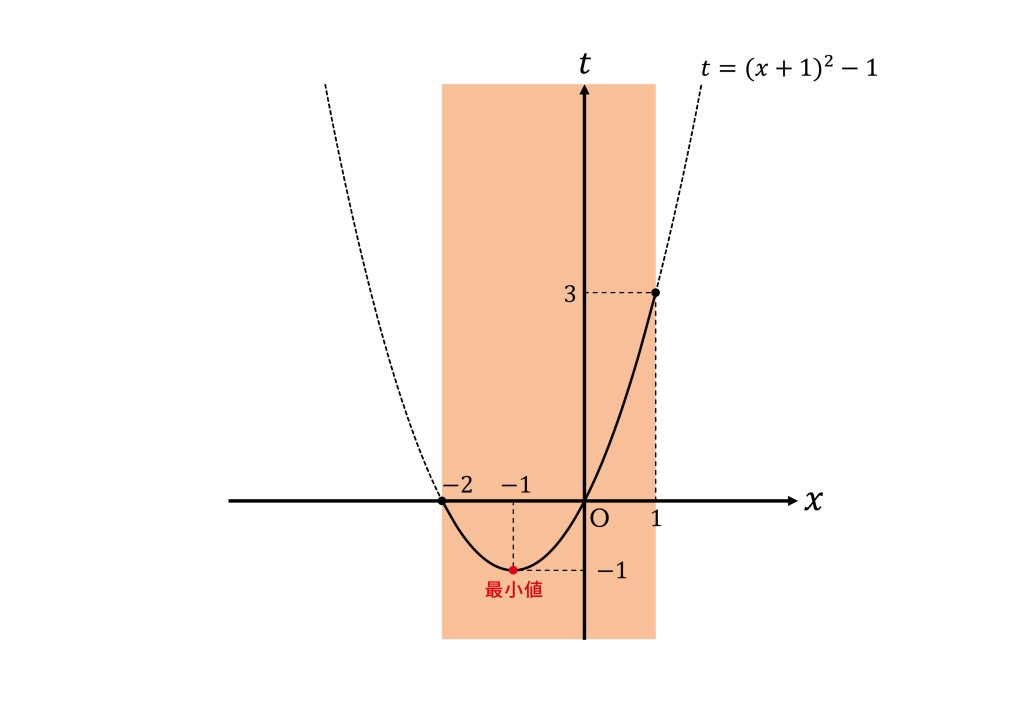
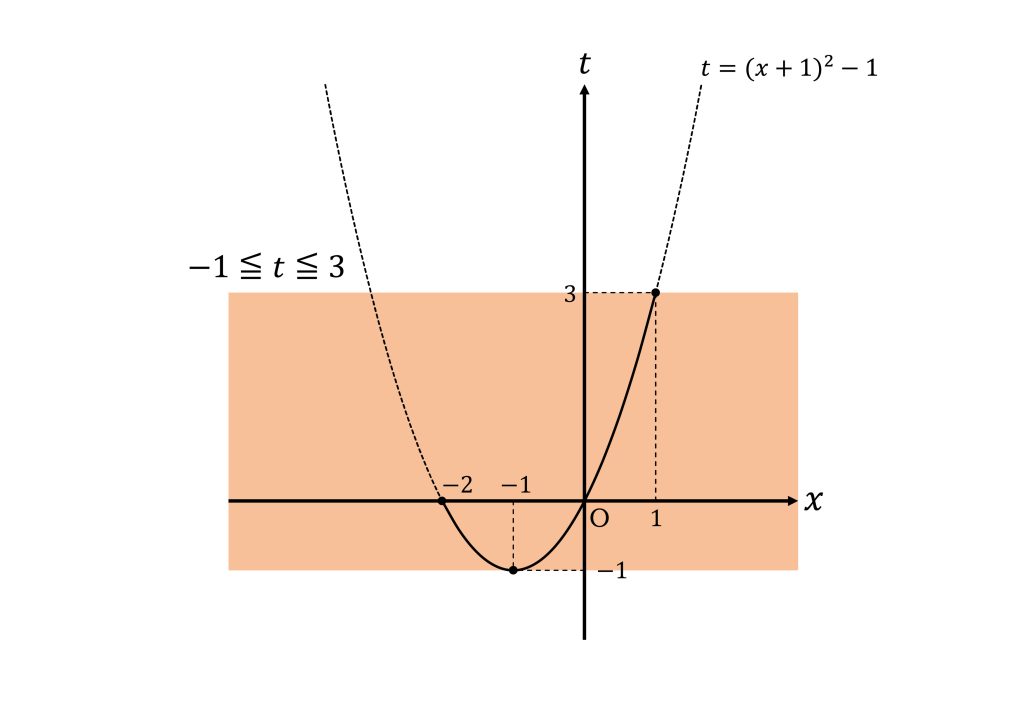
定義域が\(-1≦t≦3\)のとき\(y=(t+3)(t-2)-5t+2\)の最大値と最小値がどうなるかを考える。
\(y=(t+3)(t-2)-5t+2\)を展開して平方式に平方完成する。
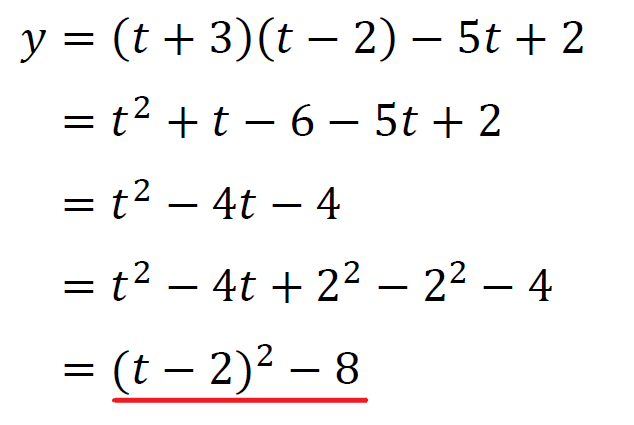
ここでまた2次関数の最大値と最小値の考え方を取り入れる。
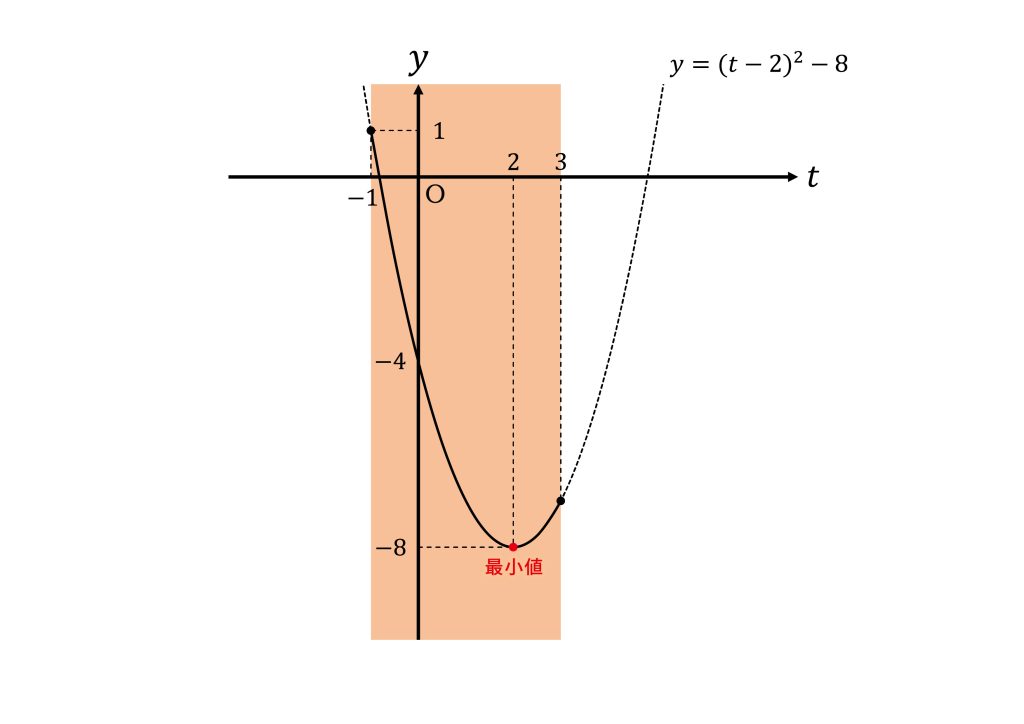
\(t\)の変域が\(-1≦t≦3\)であることから
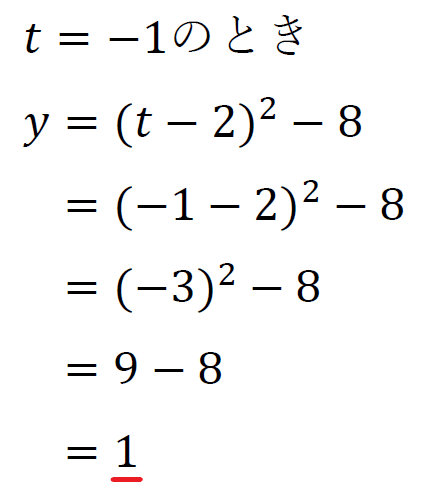
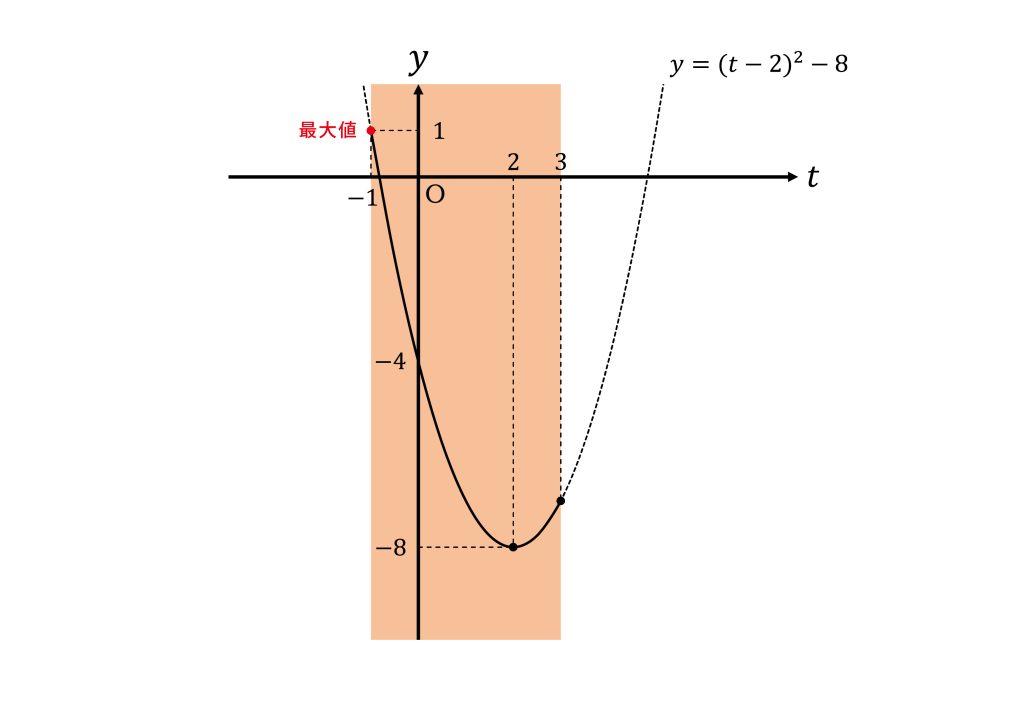
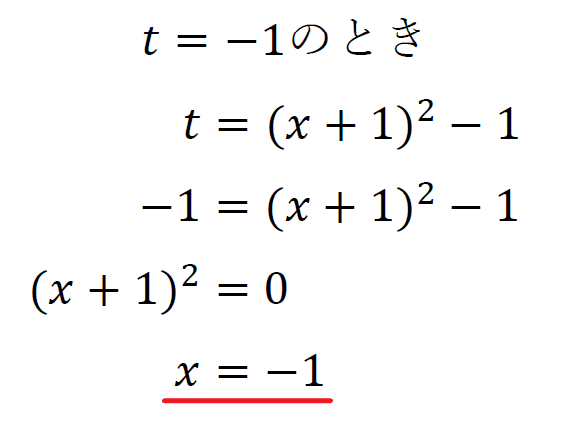
頂点\((2,-8)\)は\(-1≦t≦3\)内にあるので\(t=3\)で最小値\(-8\)をとる。
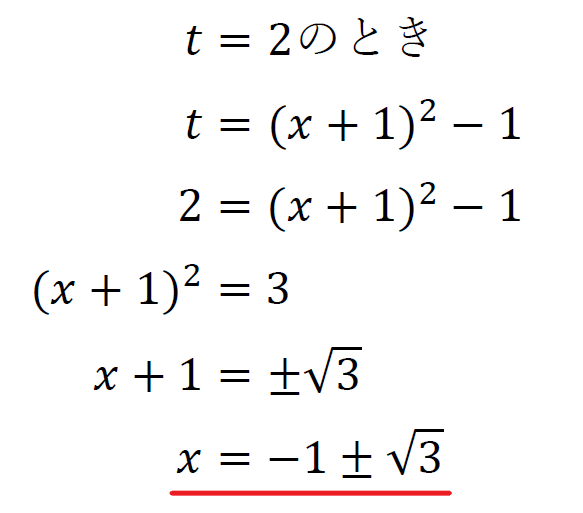
\(x=-1+\sqrt{3}\)で最小値\(-8\)をとる。
まとめると、
\(x=-1\)のとき最大値\(1\)
\(x=-1+\sqrt{3}\)のとき最小値\(-8\)
これが答え。
1.共通の式を置き換え
2.変域の確定
3.\(y\)の最大値と最小値を求める
この3ステップで複2次式の4次関数を解くことができる。
最後に\(x\)の値を求めることを忘れないようにしなければならない。
-1024x197.png)
例題を解きながら、4次関数の最大・最小の求め方を確認する。

まずは\((x^2-6x)^2+12(x^2-6x)+30\)で\(x^2-6x\)という式が共通していることを見つける。
\(x^2-6x=t\)と置き換える。
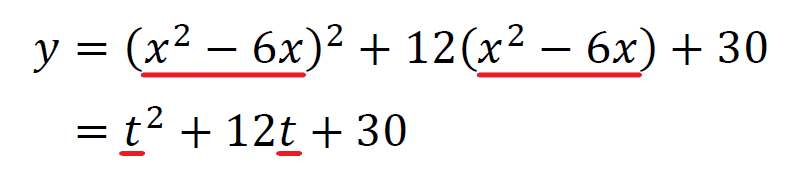
\(t\)の変域を確定させるために平方式に平方完成する。
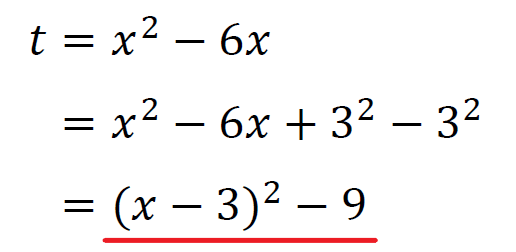
ここで2次関数の最大値と最小値の考え方を取り入れる。
所与の条件より\(1≦x≦5\)であることから
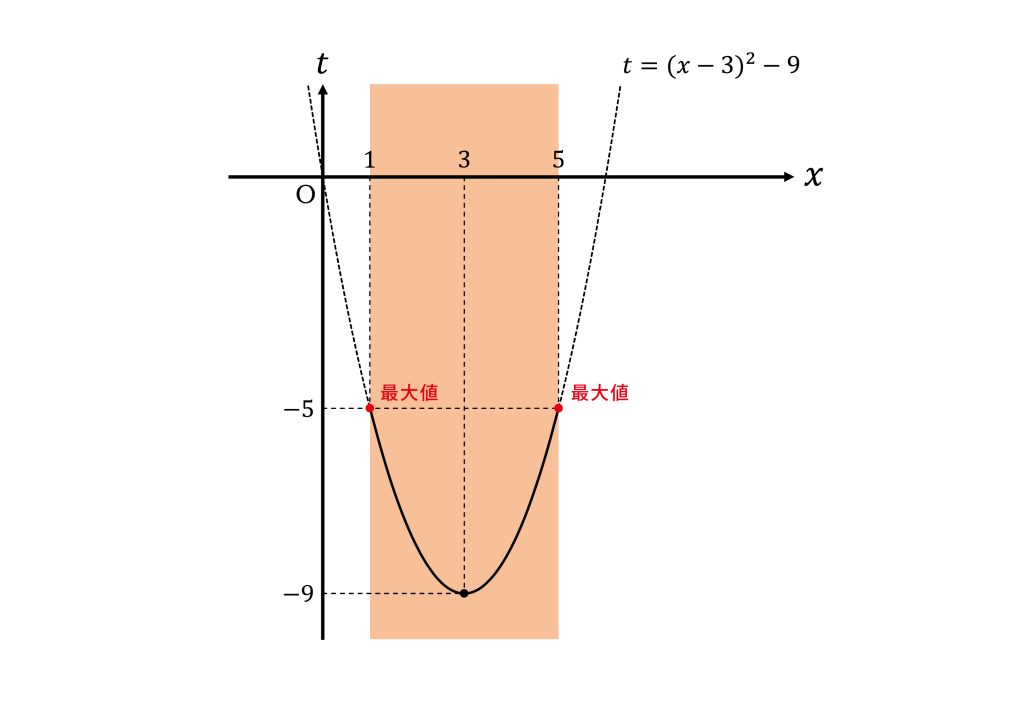
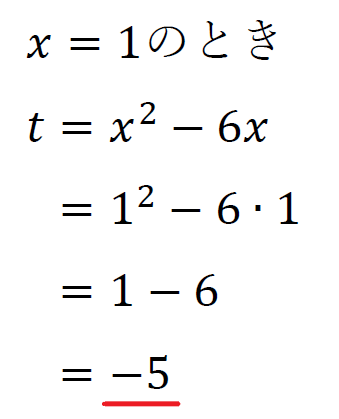
頂点\((3,-9)\)は\(1≦x≦5\)内にあるので\(x=3\)で最小値\(-9\)をとる。
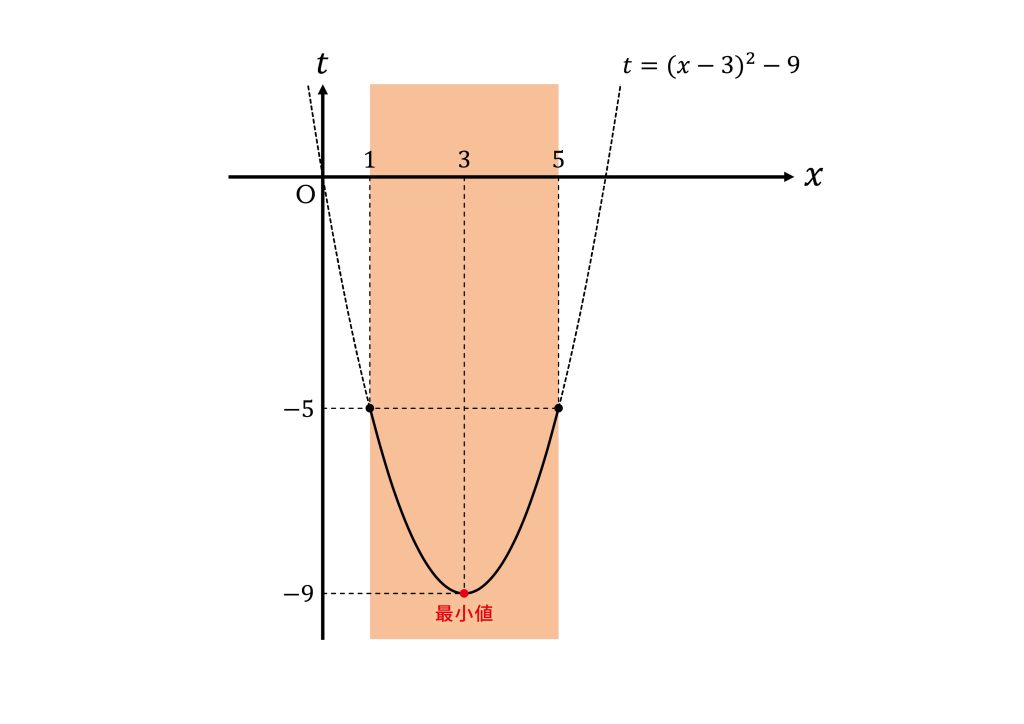
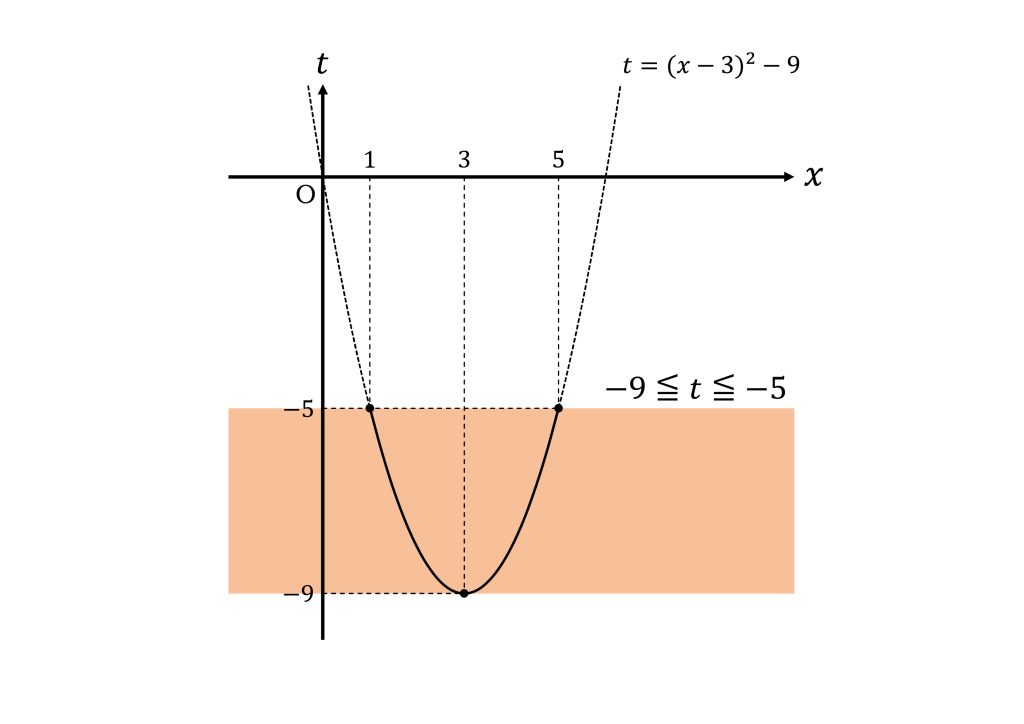
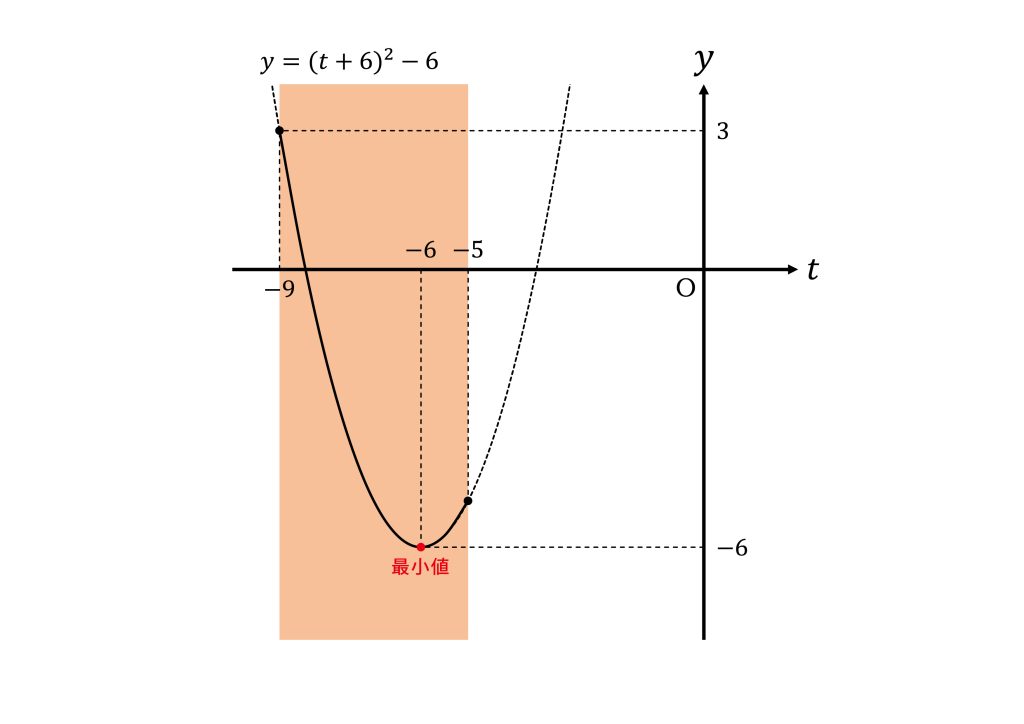
定義域が\(-9≦t≦-5\)のとき\(y=t^2+12t+30\)の最大値と最小値がどうなるかを考える。
\(y=t^2+12t+30\)を平方式に平方完成する。
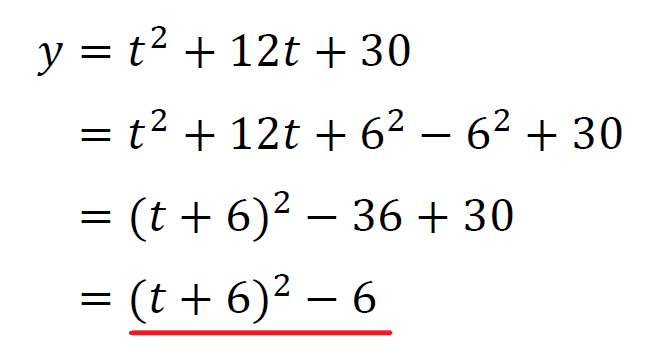
ここでまた2次関数の最大値と最小値の考え方を取り入れる。
\(t\)の変域が\(-9≦t≦-5\)であることから
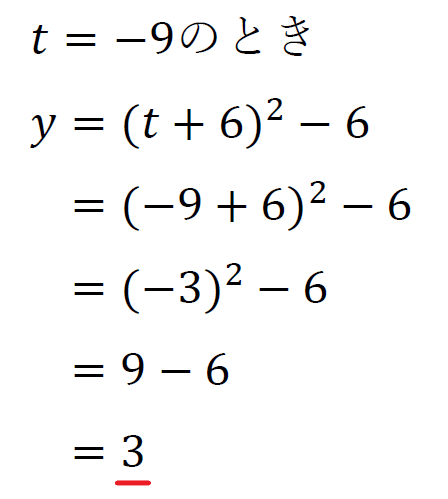
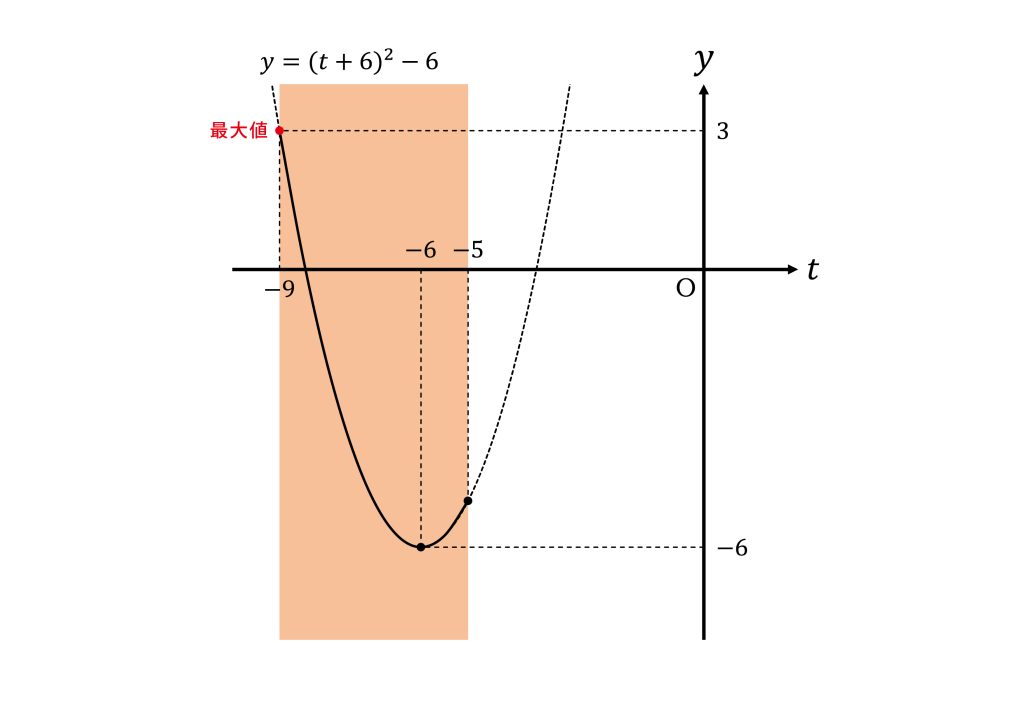
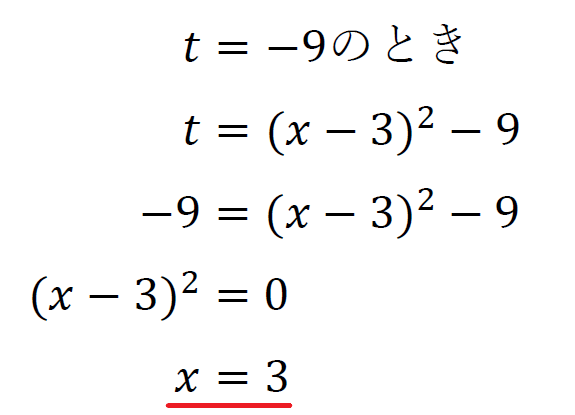
頂点\((-6,-6)\)は\(-9≦t≦-5\)内にあるので\(t=-6\)で最小値\(-6\)をとる。
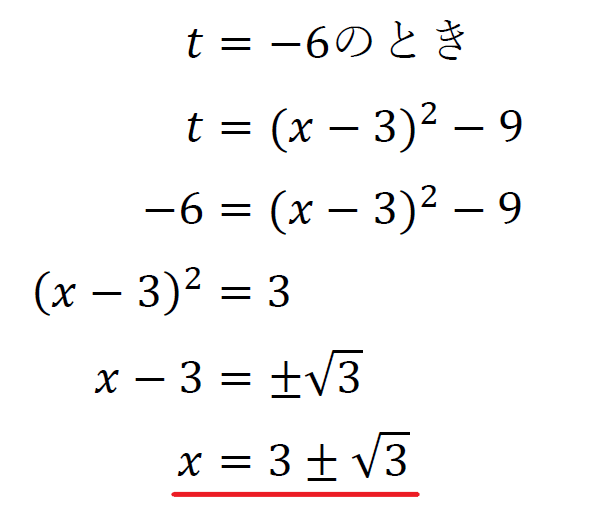
まとめると、
\(x=3\)のとき最大値\(3\)
\(x=3±\sqrt{3}\)のとき最小値\(-6\)
これが答え。
-1024x218.png)
| どんな数にでもなり得る文字のこと。変化する数。\(x\)とか\(y\)とかとか。 | |
| 最も次数の高い項の次数が「4」の式のこと。 | |
| 数の関係性のこと。 | |
| 4次式の関数。 \(y=x^4+4x^3+3x^2-2x-6\)こんな感じの関数。 |
|
| \(x^4\)と\(x^2\)と定数項のみからなる4次式のこと。 |
-1024x691.png)
2.変域の確定
3.yの最大値と最小値を求める
この3ステップで複2次式の4次関数を解くことができる。
最後に置き換えた\(t\)から\(x\)の値を求めるを忘れずに。
 すうがくのいえ
すうがくのいえ