すうがくのいえ 
「2次不等式とは？グラフから理解する基本的な解き方」で2次不等式のグラフを使った基本的な解き方が分かった。
今度は、解から成り立つ2次不等式を考えてみる。
目次
読んで字のごとく「解から係数を決定する」というそのままの意味って感じ。
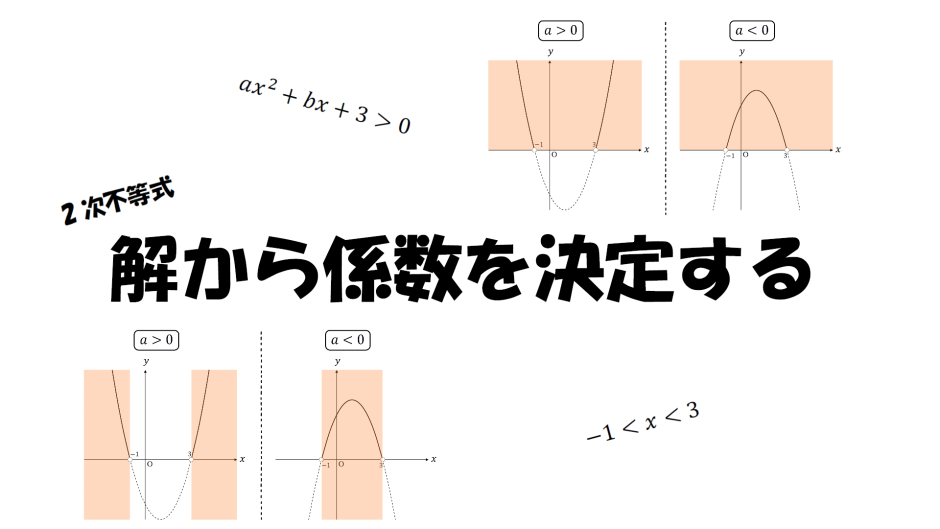
例えば、2次不等式\(ax^2+bx+3\)＞\(0\)の解が\(-1\)＜\(x\)＜\(3\)となるとき、定数\(a,b\)の値を定めることを「解から係数を決定する」という。
2次不等式を解いて解を求める作業とは逆のことをする感じ。
\(ax^2+bx+3\)＞\(0\)の左辺から\(y=ax^2+bx+3(a≠0)\)とおく。
\(-1\)＜\(x\)＜\(3\)という解から\(y=0\)のとき\(x=-1,3\)ということが分かる。
共有点が2個あることがわかるのでグラフで見てみる。
\(y\)＞\(0\)は\(x\)軸の上部分が範囲。
これを解くと
\(-1\)＜\(x\)＜\(3\)を解とする2次不等式の1つが\((x+1)(x-3)\)＜\(0\)であることを利用する。
\((x+1)(x-3)\)＜\(0\)の左辺を展開して整理する。
\((x+1)(x-3)\)＜\(0\)
\(x^2-2x-3\)＜\(0\)
与式\(ax^2+bx+3\)＞\(0\)と比較するため、両辺に\(-1\)を掛けて定数項\(3\)をそろえる。
\(x^2-2x-3\)＜\(0\)
\(-x^2+2x+3\)＞\(0\)
\(ax^2+bx+3\)＞\(0\)と\(-x^2+2x+3\)＞\(0\)を比較すると
これが答え。
☆係数比較の注意
2次不等式の解が一致するからといって、係数もすべて等しいとは限らない。例えば、
\(2x^2-4x-6\)＜\(0\)
という2次不等式の解は
\(-1\)＜\(x\)＜\(3\)
となる。これはさっき求めた\(a,b\)を代入した式\(-x^2+2x+3\)＞\(0\)の解と同じになる。\(2x^2-4x-6\)＜\(0\)と\(-1\)＜\(x\)＜\(3\)について、解は同じだけど係数はすべて違うということが分かる。つまり、2つの2次不等式
\(ax^2+bx+c\)＜\(0\)
\(a’x^2+b’x+c’\)＜\(0\)
の解が等しいからと言って、すぐに「\(a=a’,b=b’,c=c’\)」とはならない。係数が一致するためには、「最低でも1つの係数が一致していることが条件」となる。そこから他の係数も同じかどうかを判断していくのが正しいアプローチとなる。
例題を解きながら、2次不等式の解から係数を決定するやり方を確認する。
\(ax^2-8x+b\)＜\(0\)と\(y=ax^2-8x+b\)から\(y\)＜\(0\)ということが分かる。
\(y\)＜\(0\)と\(1\)＜\(x\)＜\(3\)という解から\(a\)＞\(0\)ということが分かる。
次に、\(1\)＜\(x\)＜\(3\)という解から\(y=0\)のとき\(x=1,3\)ということが分かるので、\(y=ax^2-8x+b\)に代入すると、 \[ \left\{ \begin{array}{l} \displaystyle 0=a-8+b\\ 0=9a-24+b \end{array} \right. \] という連立方程式が成り立つ。
これを解くと
グラフで見ると
別解として、\(1\)＜\(x\)＜\(3\)を解とする2次不等式の1つが\((x-1)(x-3)\)＜\(0\)であることを利用する。
これが答え。
\(2ax^2+2bx+4\)≦\(0\)と\(y=2ax^2+2bx+4\)から\(y\)≦\(0\)ということが分かる。
\(y\)≦\(0\)と\(x\)≦\(-1,2\)≦\(x\)という解から\(a\)＜\(0\)ということが分かる。
次に、\(x\)≦\(-1,2\)≦\(x\)という解から\(y=0\)のとき\(x=-1,2\)ということが分かるので、\(y=2ax^2+2bx+4\)に代入すると、 \[ \left\{ \begin{array}{l} \displaystyle 0=2a-2b+4\\ 0=8a+4b+4 \end{array} \right. \] という連立方程式が成り立つ。
これを解くと
グラフで見ると
別解として、\(x\)≦\(-1,2\)≦\(x\)を解とする2次不等式の1つが\((x+1)(x-2)\)≧\(0\)であることを利用する。
これが答え。
| \(y=ax^2+bx+c\)(\(a,b,c\)は定数、\(a≠0\)) | |
|
\(ax^2+bx+c\)＞\(0\) \(ax^2+bx+c\)＜\(0\) \(ax^2+bx+c\)≧\(0\) \(ax^2+bx+c\)≦\(0\) (\(a,b,c\)は定数、\(a≠0\)) |
|
| 複数の変数を含む複数の方程式 |
2次不等式を解くことができれば、解から係数を決定するのはそれほど難しくない。
前回と同じように、ここまで学んできた2次方程式や2次関数の知識が、2次不等式の理解にもそのまま活かせる。
もし途中でつまずいたら、そのポイントの元になっている単元に戻って理解を深めていきたい。
