因数分解をするとき、扱う文字が3つになった途端、すごくややこしくなる。
見た瞬間にそっとペンを置きたくなる。
でも覚えてしまえばすごく使い勝手がいい。
なのでできれば覚えておきたい。
「2次式」と「3次式」に分けて、
文字が3つの2次式の因数分解と、
文字が3つの3次式の因数分解について見ていく。

2次式は、めちゃくちゃ噛み砕いていうと「2乗の式」って感じ。
まずは、展開の公式1.を変形していく。
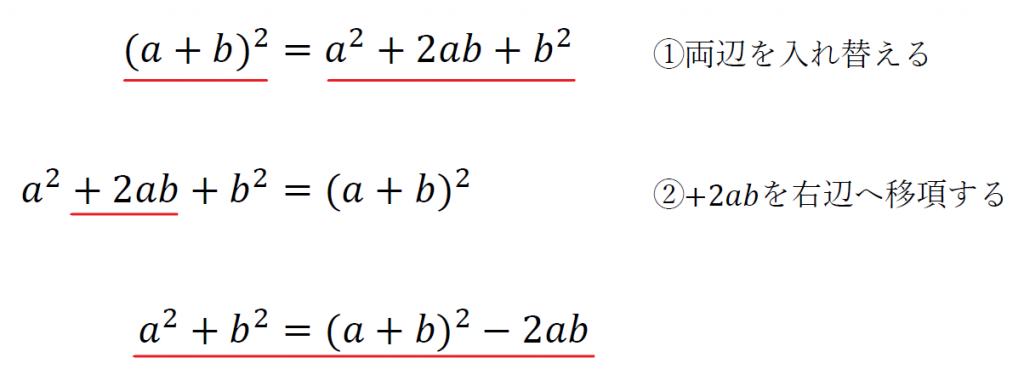
こんな感じに変形することができる。
これを前提に、文字が3つの2次式の因数分解を考える。
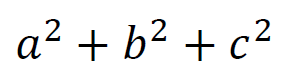
こんな感じの式が、3文字の2次式。
この式を因数分解してみる。

こんな感じになる。
これは一つの公式として覚えておきたい。
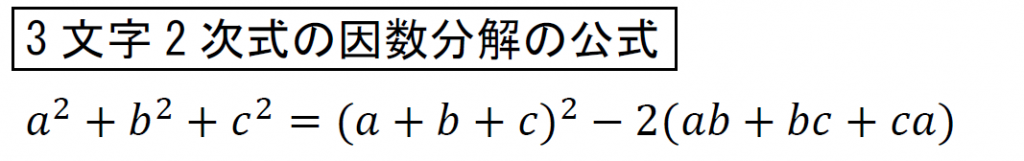
これで、文字が3つの2次式の因数分解ができた。
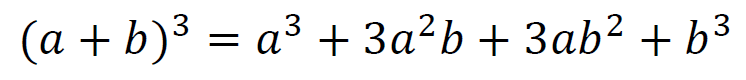
今度は3次式を考えてみる。
3次式は、めちゃくちゃ噛み砕いていうと「3乗の式」って感じ。
まずは、展開の公式6.を変形していく。
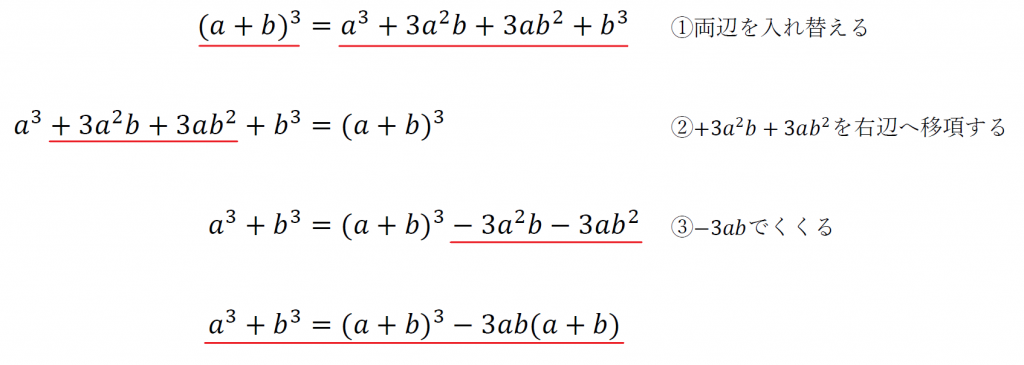
こんな感じに変形することができる。
これを前提に、文字が3つの3次式の因数分解を考える。
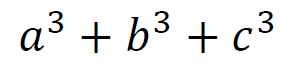
こんな感じの式が、3文字の3次式。
この式を因数分解してみる。

こんな感じになる。
長くて長いから疲れる。
ムズイ。
公式として覚えるときは、また少し式を変形させる。
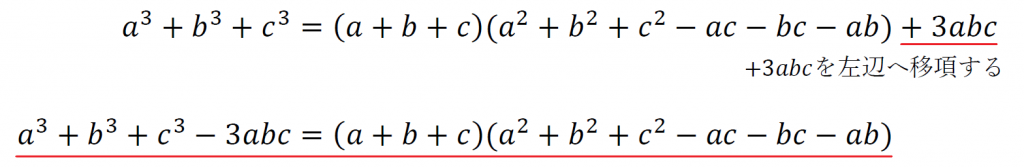
覚えるときはこの形で覚える。
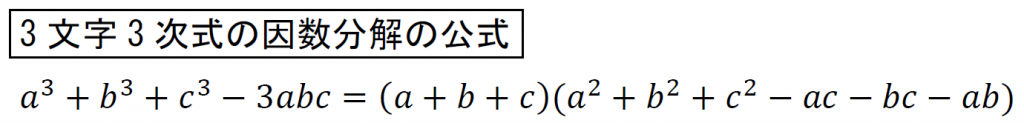
これで、文字が3つの3次式の因数分解ができた。
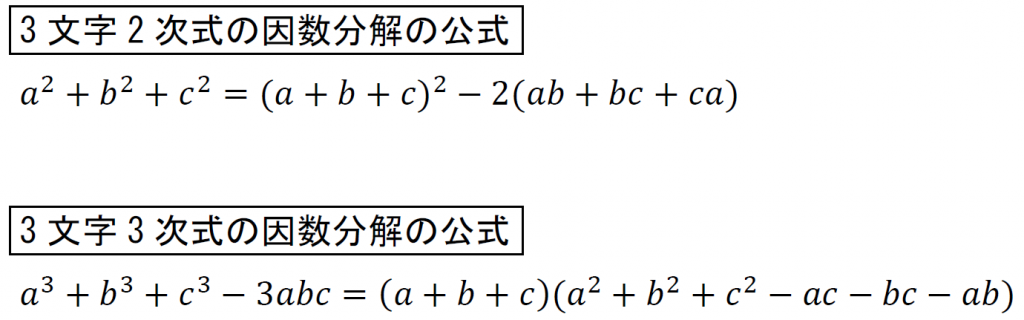
これらの公式はできれば覚えておきたい。
覚えると同時に、公式の導出ができるようにしておきたい。

文字が3つの因数分解は結構難しいイメージ。
難しいから、公式として覚えておいた方が良いと思っていても、公式すらちょっと長くてややこしい。
やっかい。
といっても、いざ問題として出てきたときに公式を覚えていないと、かなり苦労する。
なので、長くてややこしくても覚えておきたい。
覚えておきたい…!
今回の公式に限らず、大体の公式はすぐ使えるようにするため暗記しておくことが多い。
暗記しておくことで、実際の問題で具体的な数字を公式に当てはめて早く解くことができる。
でもたまに公式の使いどころが分からなかったりすることもある。
そういうときは、新しいパターンとして解き方の「型」を覚えるようにする。
そうすれば答えへの道が光って見えるようになる。
公式自体が暗記しにくいということもよくある。
暗記しておくことより、なぜそうなるのかを理解しておくことの方が大事だ。
そうすれば、一度覚えれば忘れにくくなるし、覚え間違いをしなくなる。
たまに思い出して、何故公式の形になったのかを一から計算し直してみてもいいかも。
 すうがくのいえ
すうがくのいえ 


Twitter/X でこのページを紹介している人がいて読みにきたのです
が、
a^2+b^2+c^2=(a+b+c)^2 – 2(ab+bc+ca)
という式変形を「因数分解」と呼ぶのは誤りですね。
積に表されているわけではありませんから。
(基本対称式を用いて表す、みたいな呼び名で習うことはあります。)
≪…因数分解…≫について、すべての自然数は、因数分解できている。との記事を見つける。
( (exp[n+1]-exp[n]) /exp[n] )×( ( (e-1)/(e-2) )
= (e-1)((e-1)/(e-2))
『創発直方体』の[体積]の『保型』
これが、 i × i=-1=exp[iπ] とのコト。
( (exp[n+1]-exp[n]) /exp[n] )×( ( (e-1)/(e-2) )
⇔ [-1] になる。
このナラティブは、絵本の力で・・・
もろはのつるぎ (有田川町電子図書館)