すうがくのいえ 
方程式の実数解の個数から定数を求める問題は、一見すると「不等式」とは無関係に見える。
だけど、実数解の条件を満たす定数を求めるには、結局のところ2次不等式を解かざるを得ないケースが多い。
問題文に「不等式を解け」と書いていなくても、自分で2次不等式を設定して解く必要があることに注意したい。
2次不等式とは？グラフから理解する基本的な解き方
目次
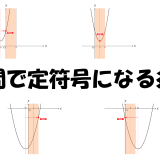
この判別式\(D\)の符号によって
①\(D\)＞\(0\)のとき実数解は2個
②\(D\)＝\(0\)のとき実数解は1個
③\(D\)＜\(0\)のとき実数解は0個
この中のどれかになる。
判別式の使い方
2次方程式\(x^2-(k+1)x+1=0\)より
\(D=k^2+2x-3\)より\(k^2+2x-3\)＞\(0\)となるので
判別式は、2次方程式における実数解の個数を判別するので、2次方程式以外では使えないということにも注意しなきゃいけない。
判別式は2次方程式でしか使えない
例題を解きながら、実数解の個数から定数を求めるやり方を確認していく。
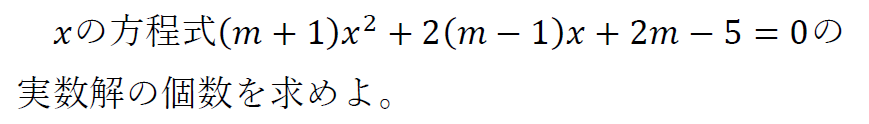
なので、\([1]m+1=0\)のときと\([2]m+1≠0\)のときで、場合分けをして解いていく。
\([1]m+1=0\)のとき
\(m+1=0\)より
けど、一応代入してみる。
\([2]m+1≠0\)のとき
\(m+1≠0\)より
①\(D\)＞\(0\)
②\(D\)＝\(0\)
③\(D\)＜\(0\)
の3パターンで考える。
①\(D\)＞\(0\)のとき実数解は2個
②\(D\)＝\(0\)のとき実数解は1個
③\(D\)＜\(0\)のとき実数解は0個
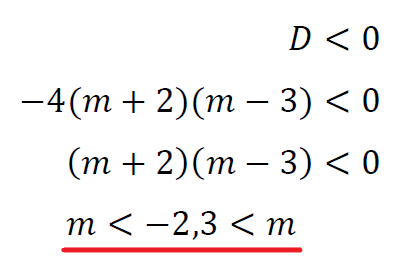
\([1]\)と\([2]\)を合わせて
\(-2\)＜\(m\)＜\(-1,-1\)＜\(m\)＜\(3\)のとき2個
\(m=-2,-1,3\)のとき1個
\(m\)＜\(-2,3\)＜\(m\)のとき0個
これが答え。
|
\(ax^2+bx+c\)＞\(0\) \(ax^2+bx+c\)＜\(0\) \(ax^2+bx+c\)≧\(0\) \(ax^2+bx+c\)≦\(0\) (\(a,b,c\)は定数、\(a≠0\)) |
|
| \(ax^2+bx+c=0\) | |
| \(D=b^2-4ac\) | |
| ①\(D\)＞\(0\)のとき実数解は2個 ②\(D\)＝\(0\)のとき実数解は1個 ③\(D\)＜\(0\)のとき実数解は0個 |
実数解の個数を条件にした問題は、とりあえず判別式を活用するのが基本となる。
判別式の不等式を立てる際は、2次不等式を正しく解ける力が問われる。
問題文の中で「方程式」とだけ表現されている場合は、必ずしも2次方程式になるとは限らない。
その場合は、与えられた式の次数や問題の構造に応じて、場合分けをする必要がある。
結構見落としやすいポイントなので、忘れずにしっかり問題文の意図を汲んでいきたい。
