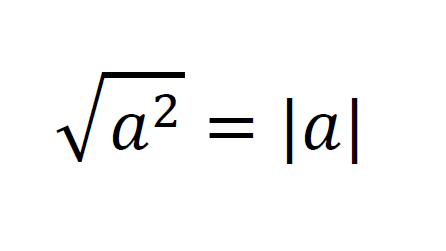ルートの計算をする中で、素因数分解をして平方因数を外に出すことで、簡単な値に表すことができる。
計算の途中で使えれば計算が楽になるし、
計算結果でも簡単な値に表すことができるのであれば簡単な値に表しておきたい。

まずは、素因数分解をして平方因数を外に出す作業で出てくる登場人物のご紹介。
なんか難しそうな人たち。
順番に確認していこう。

因数とは、因数分解後の積を作っている各式のこと。

因数分解とは、1つの多項式を1次以上の多項式の積の形に変形すること。
つまり足し算を掛け算に変形すること。

素数とは、その数自身と、1以外に約数を持たない自然数(ただし1を除く)のこと。
順番に見ていくと何が素数か分かりやすいかも。

こんな感じ。
あと17と19も素数。
とりあえずそれくらい覚えておけばいい感じ。

素因数分解とは、ある正の整数を素数の積の形で表すこと。
因数分解の素数バージョン。
つまり、素数だけの掛け算にすること。
コツとして、
・偶数であれば必ず2の倍数
・数字を全部足して3の倍数になれば必ず3の倍数
・下2桁が4の倍数であれば必ず4の倍数
・下1桁が5または10であれば必ず5の倍数
・偶数かつ数字を全部足して3の倍数になれば必ず6の倍数
これくらい覚えておけば大体は素因数分解できる。
あとは、他の素数で割り切れないか確認して割り切れなければそれで素因数分解は完了。
素因数分解は、分数の計算をする時にもとても役に立つ。

平方因数とは、素因数分解したときに、2乗の形(平方)に出来る因数のこと。
この平方因数のおかげでルートを簡単な値に表すことができる。
と、いうことを踏まえて

平方根の公式を使って、平方因数をルートの外に出す。
実際に数字を入れて計算してみると、素因数分解で平方因数をルートの外に出す作業を理解しやすい。

カッコの中の数字をそのまま外に出してマイナスにしないように注意しなければならない。

14に平方因数はない。
必ずしもすべてのルートを外せるとは限らない。

数字が増えても、1つずつ平方因数を見つけることができれば、簡単な値に表すことができる。

| 因数 | 因数分解後の積を作っている各式のこと |
| 因数分解 | 1つの多項式を1次以上の多項式の積の形に変形すること |
| 素数 | その数自身と、1以外に約数を持たない自然数(1を除く) |
| 素因数分解 | ある正の整数を素数の積の形で表すこと |
| 平方因数 | 素因数分解したときに、2乗の形(平方)に出来る因数のこと |
細かい言葉にも細かい意味がある。

素因数分解ができれば確実に計算がはかどる。
ルートを外すのもそうだけど、
分数を約分するときとか、確率の問題でも重宝する。
漢字ばっかりでムズイネ。
 すうがくのいえ
すうがくのいえ