「放物線と直線の共有点の求め方」で放物線と直線の共有点の求め方が分かった。
今度は、式の中に文字が含まれていた場合、どのように解いていけば良いか考えていく。

やることは基本的に「放物線と直線の共有点の求め方」と同じ。
違いは、計算の中に文字が入る分、整理や不等式処理が少し増えるだけ。

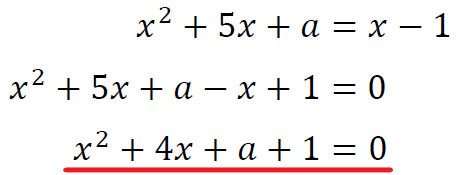
「共有点を持つ」ということは「\(D≥0\)」ということ。
なので「\(-4a+12≥0\)」という式を立てることができる。
これを解くと、
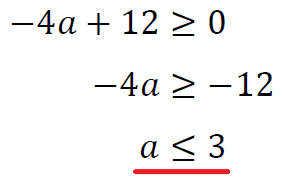
グラフで表すと
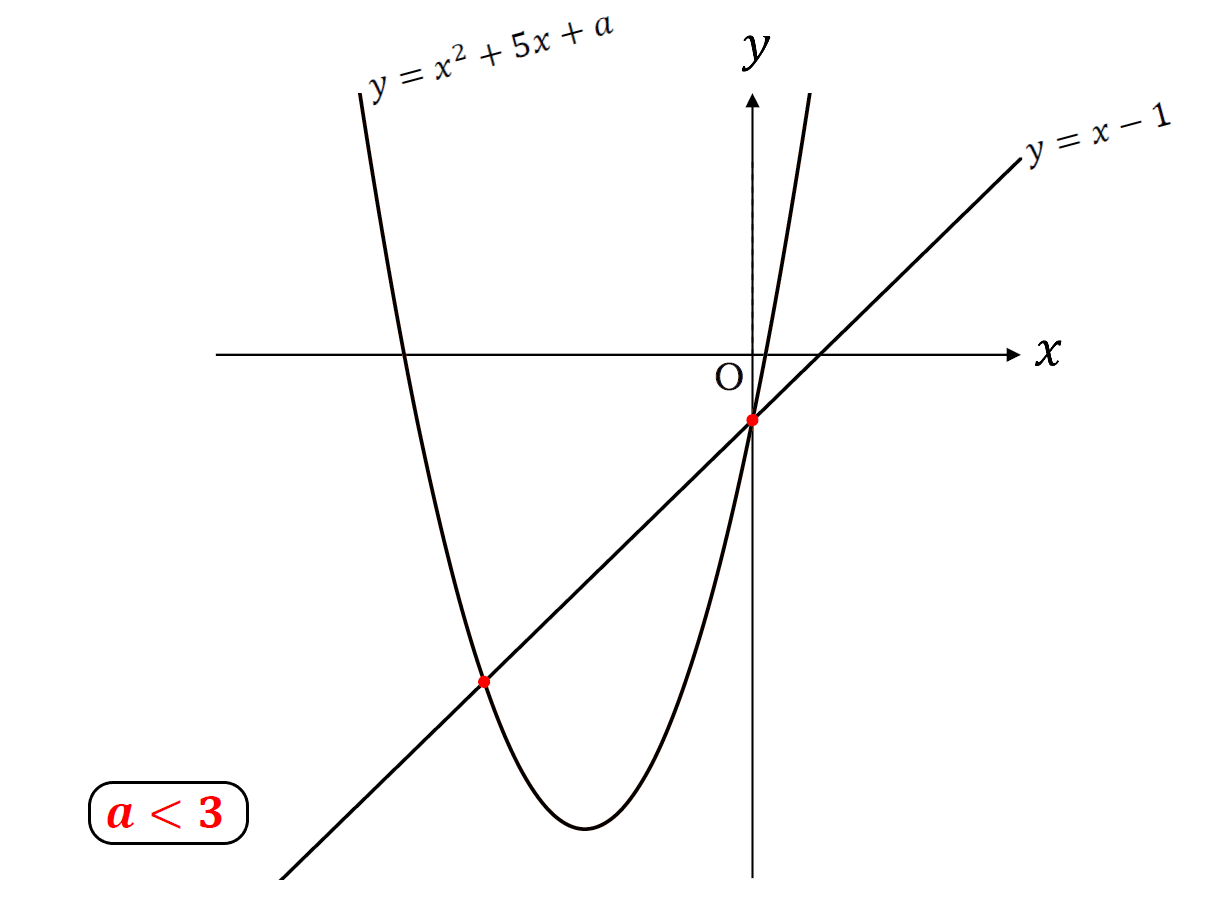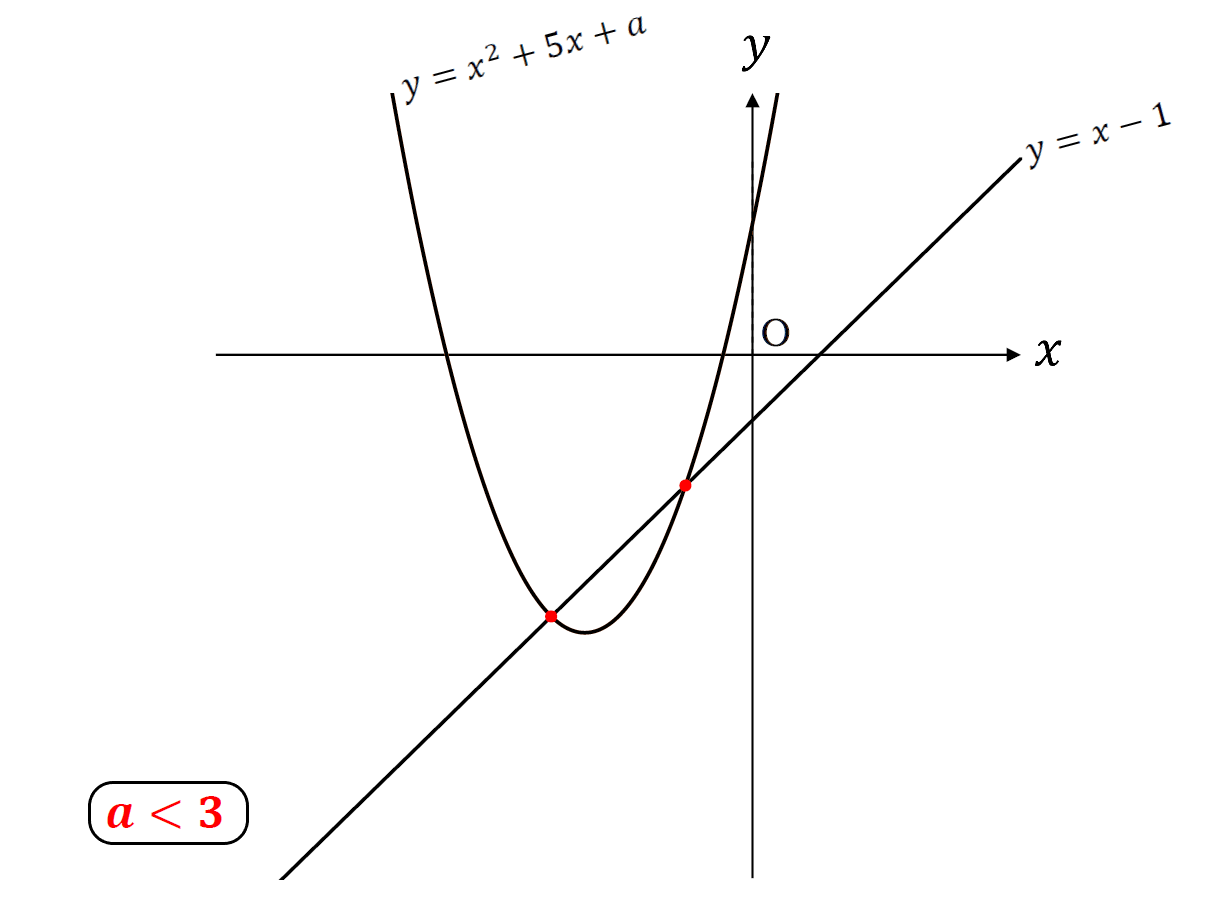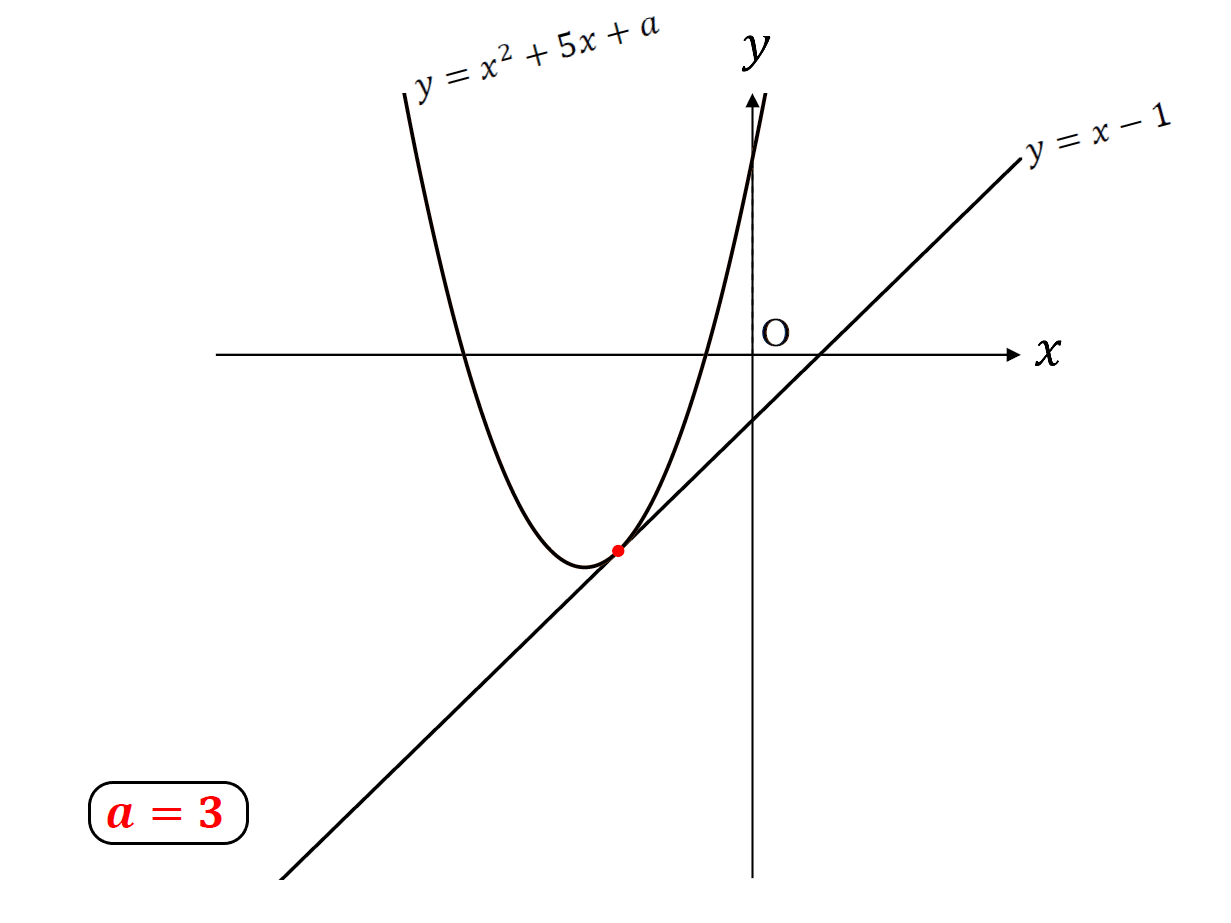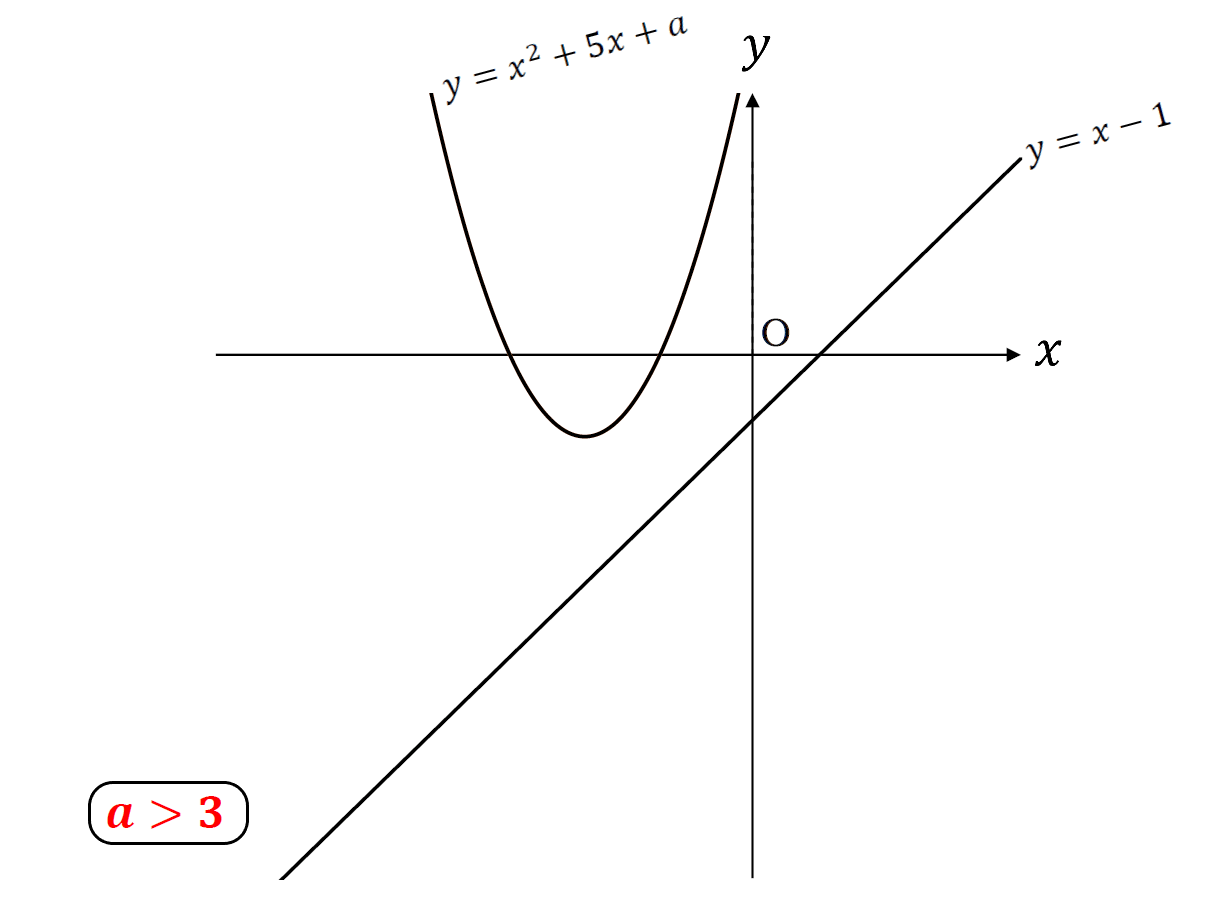
こんな感じ。

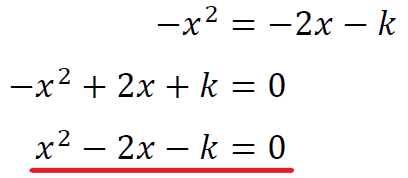
・\(D\)>\(0\)のとき、共有点2個
・\(D\)=\(0\)のとき、共有点1個
・\(D\)<\(0\)のとき、共有点なし
となるので、それぞれ場合分けして考える。
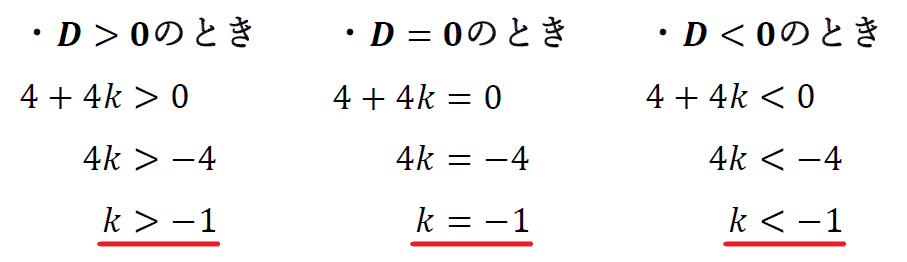
\(k\)>\(-1\)のとき共有点2個
\(k\)=\(-1\)のとき共有点1個
\(k\)<\(-1\)のとき共有点なし
これが答え。
グラフで表すと
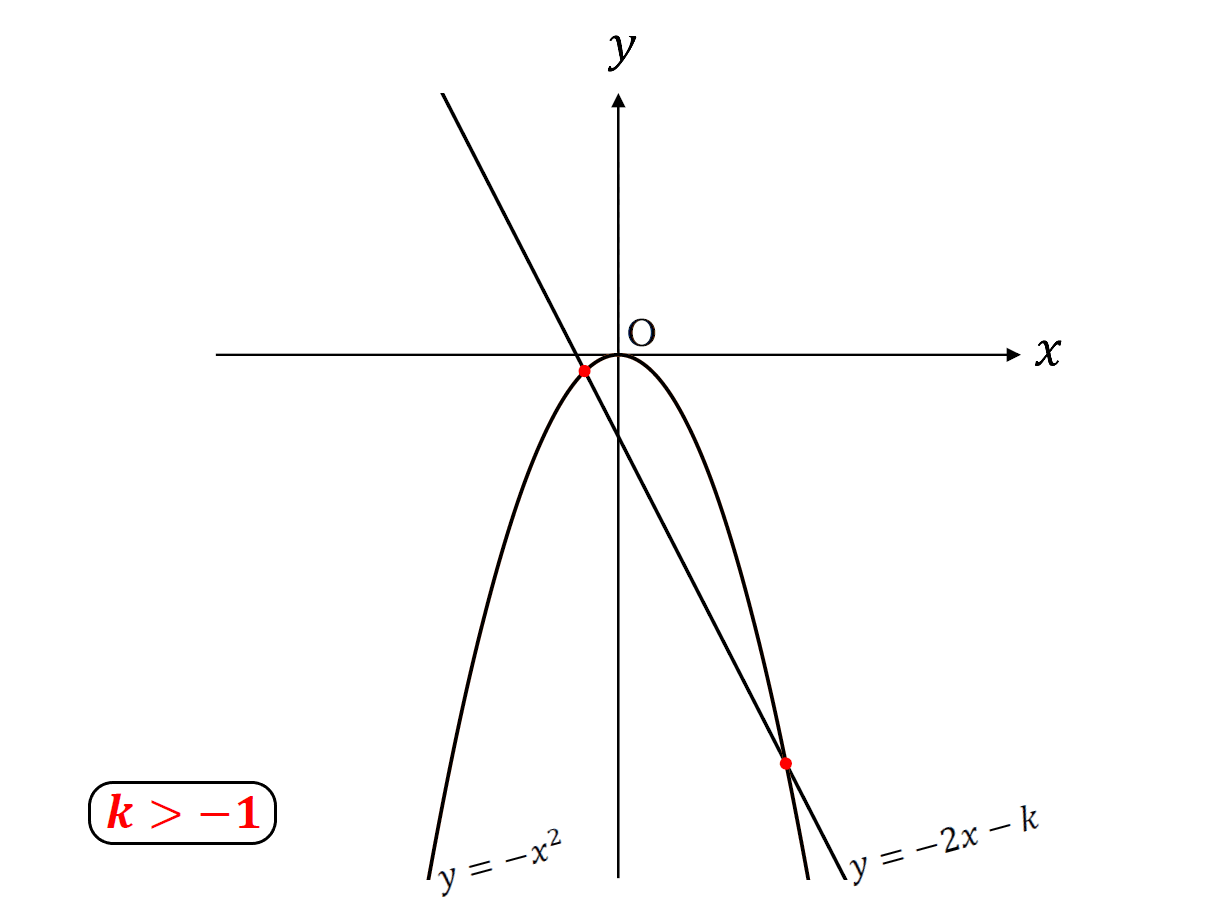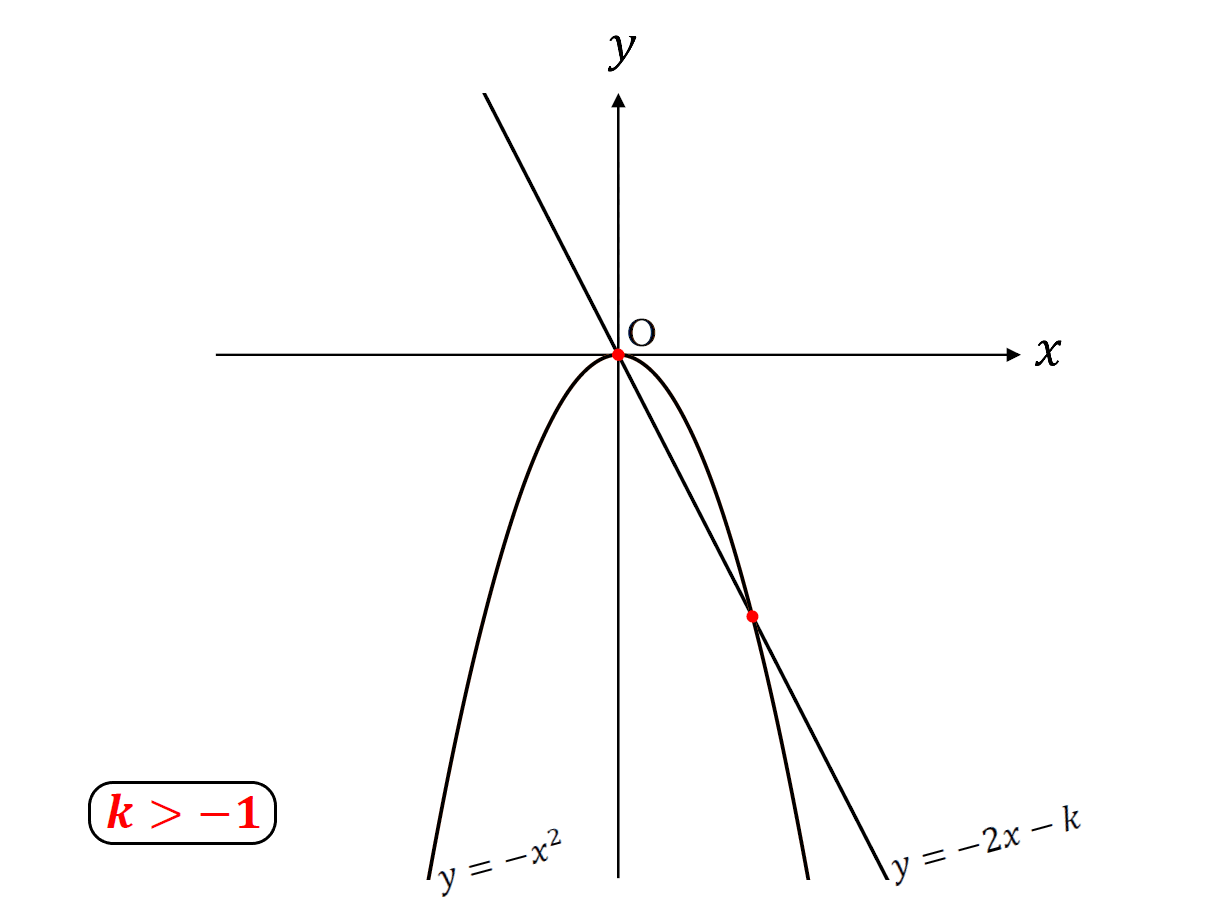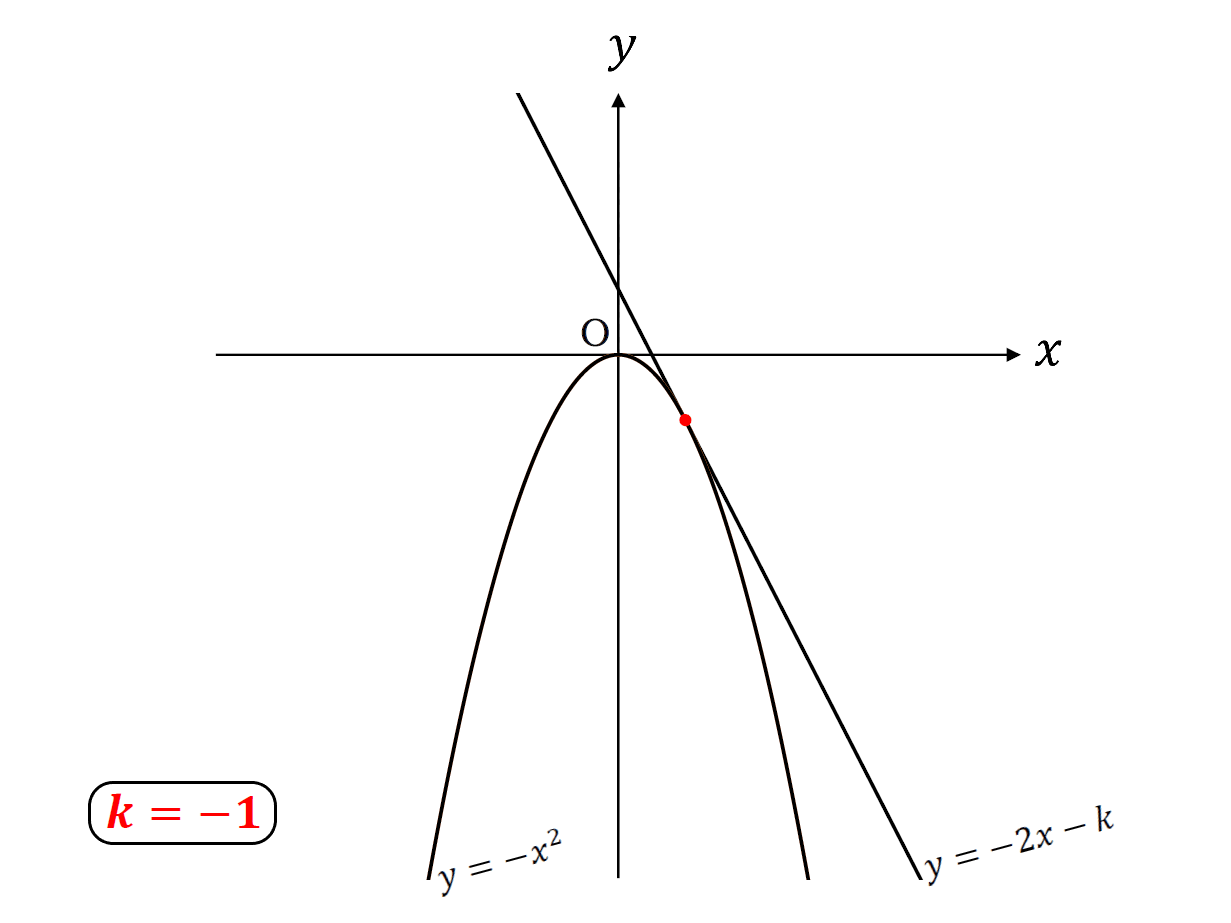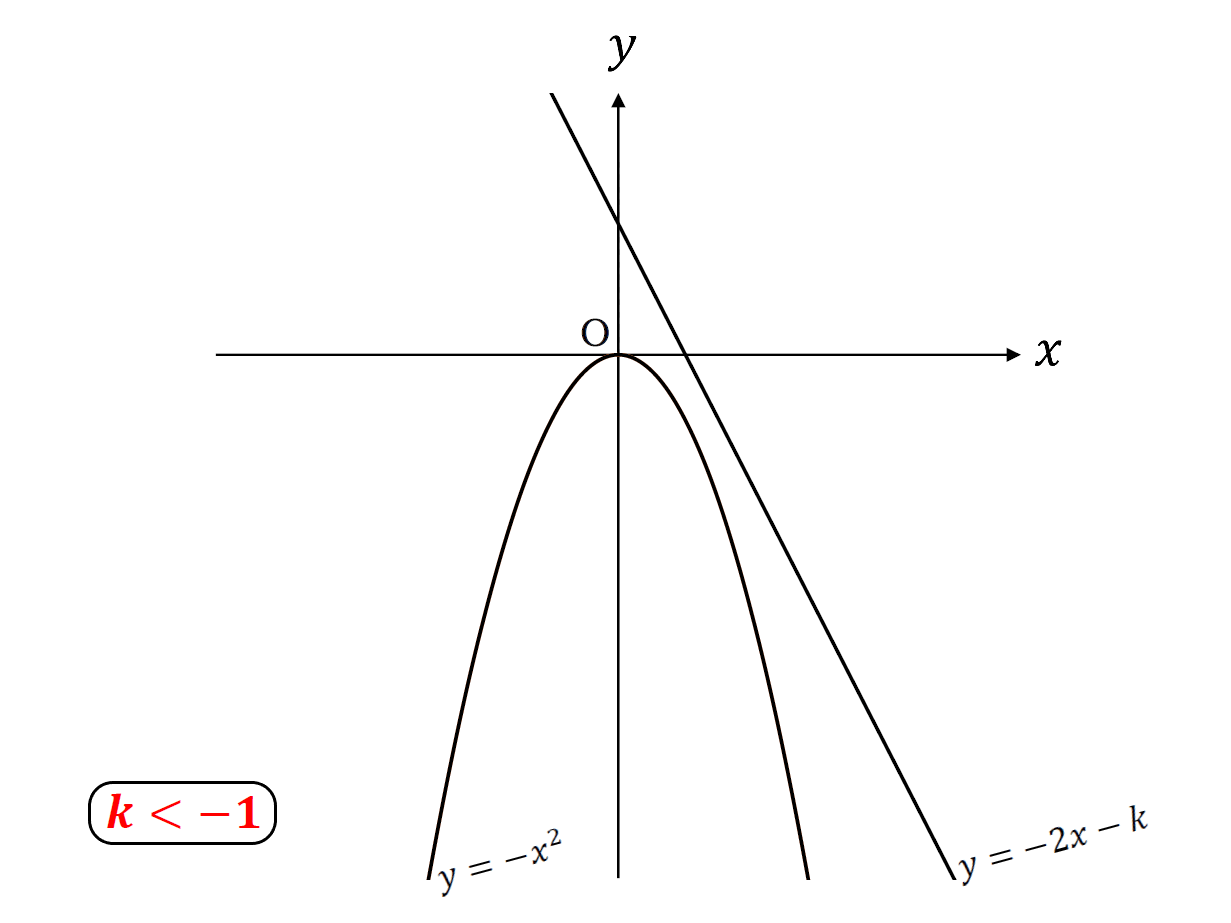
こんな感じ。
-1024x197.png)
例題を解きながら、文字を含む放物線と直線の共有点の求め方を確認する。


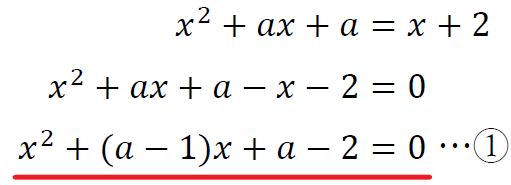
「接する」ということは「\(D=0\)」ということ。
なので「\(a^2-6a+9=0\)」という式を立てることができる。
これを解くと、
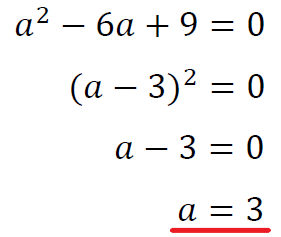
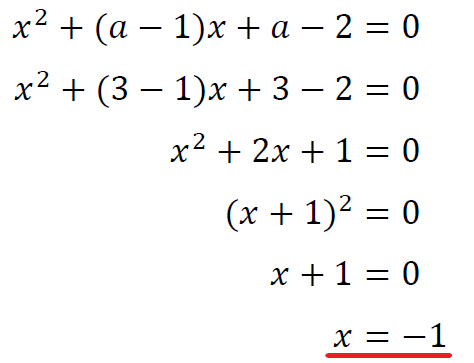
\(a=3\)のとき接点の座標は\((-1,1)\)
これが答え。
グラフで表すと
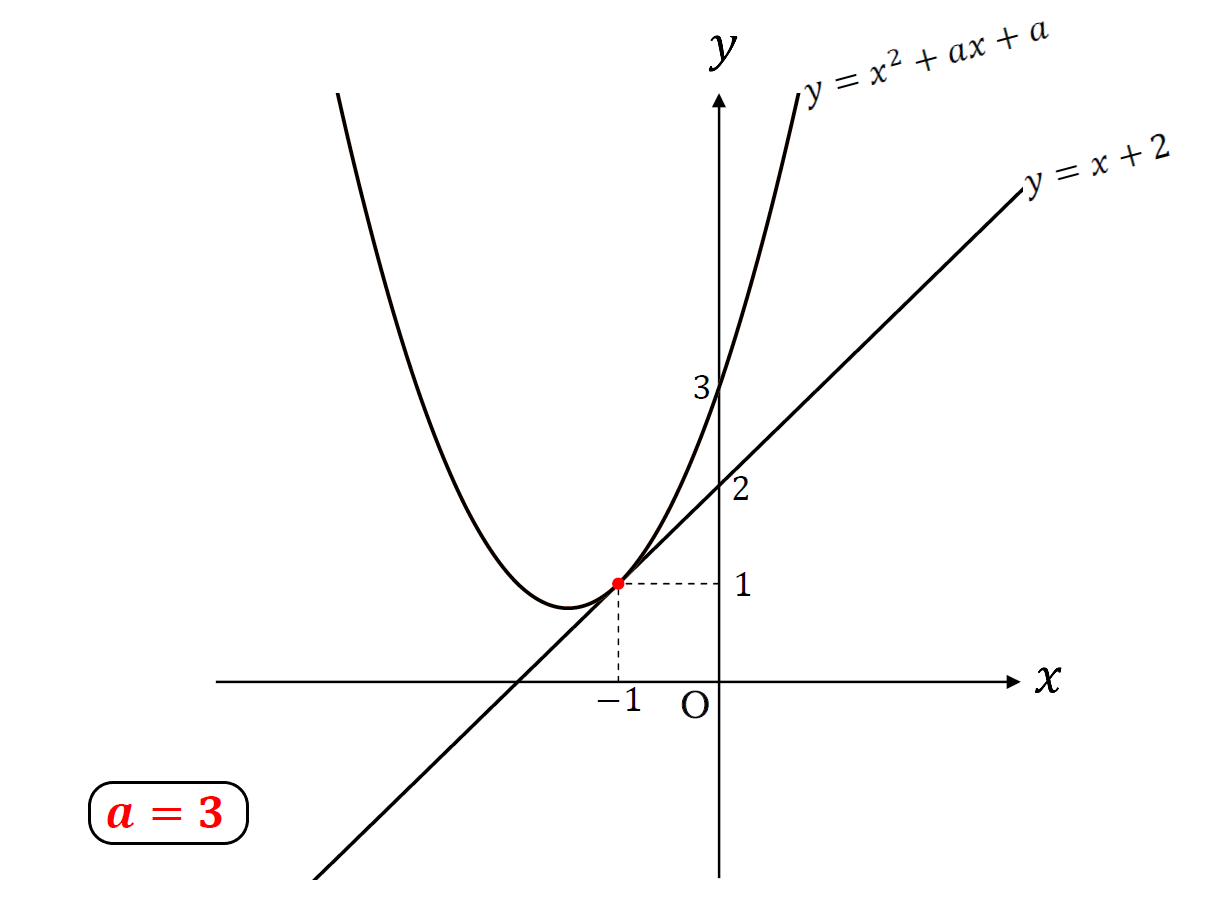
こんな感じ。

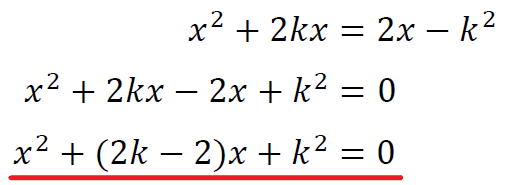
・\(D\)>\(0\)のとき、共有点2個
・\(D\)=\(0\)のとき、共有点1個
・\(D\)<\(0\)のとき、共有点なし
となるので、それぞれ場合分けして考える。
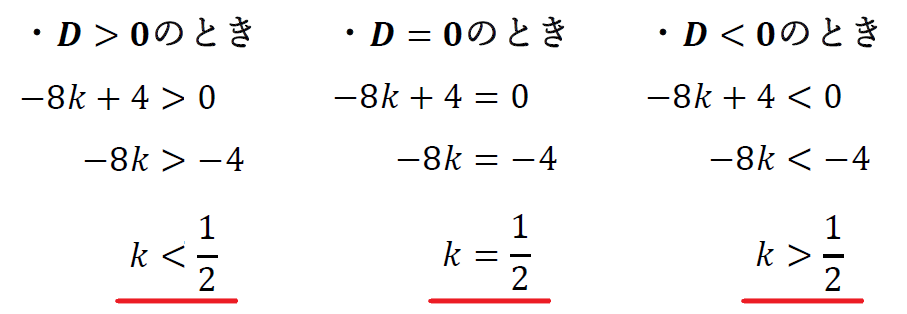
\(k\)<\(\frac{1}{2}\)のとき共有点2個
\(k\)=\(\frac{1}{2}\)のとき共有点1個
\(k\)>\(\frac{1}{2}\)のとき共有点なし
これが答え。
グラフで表すと
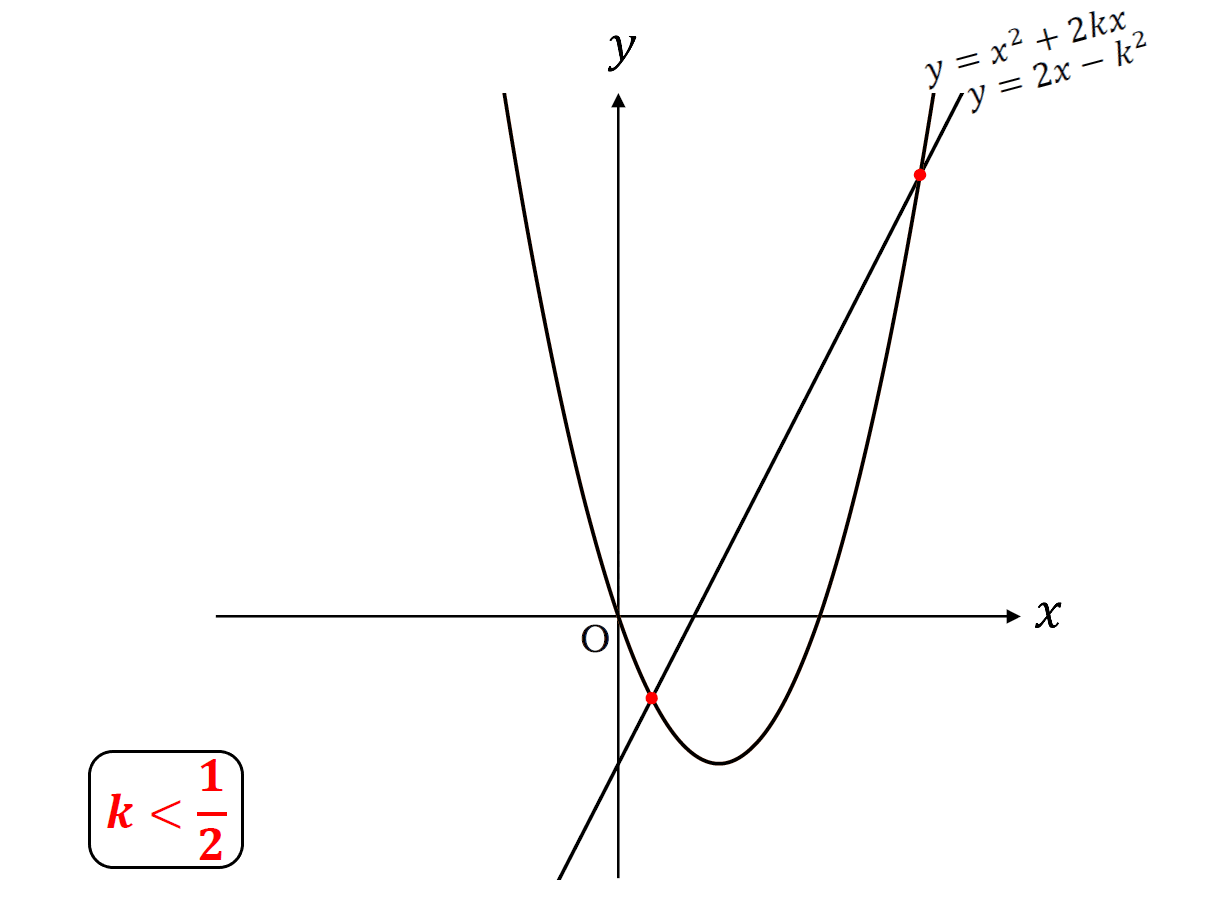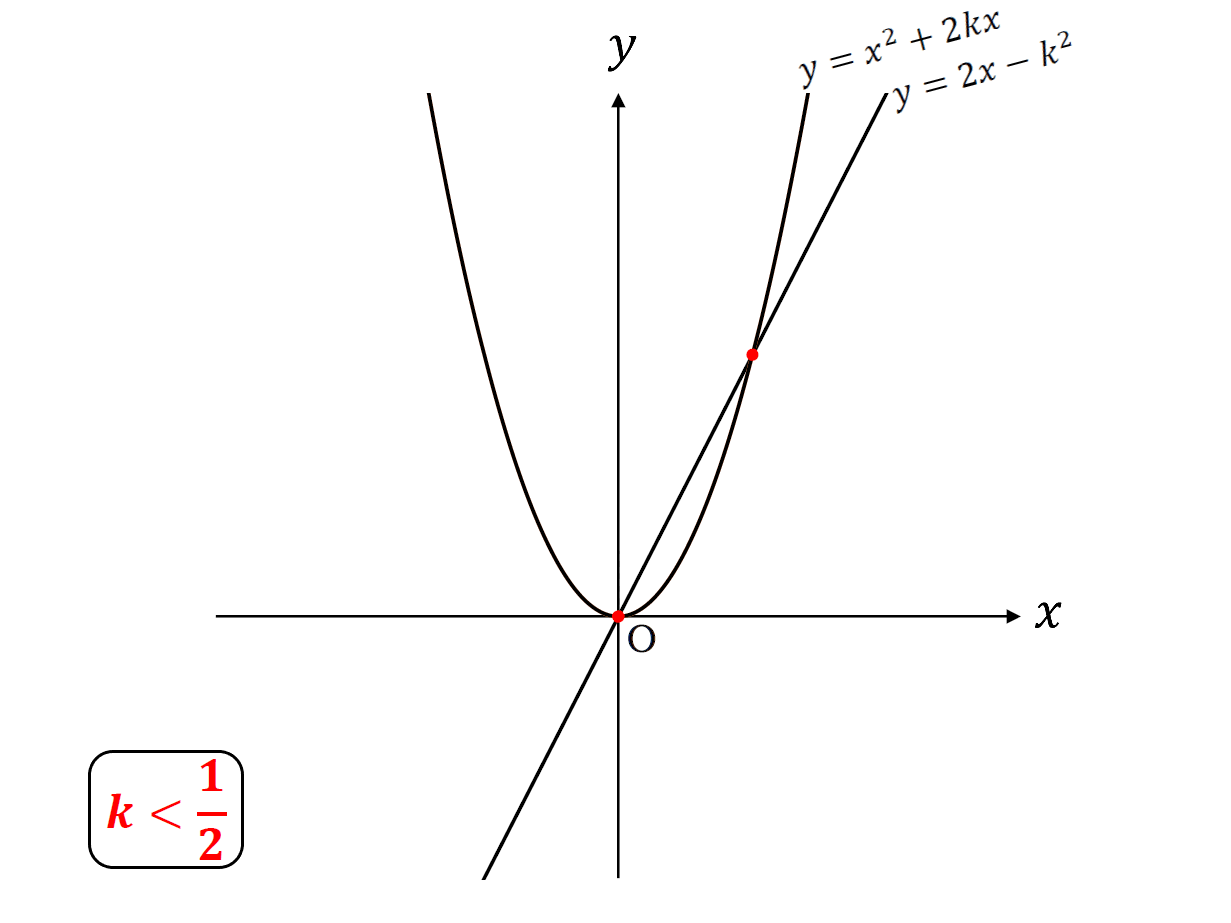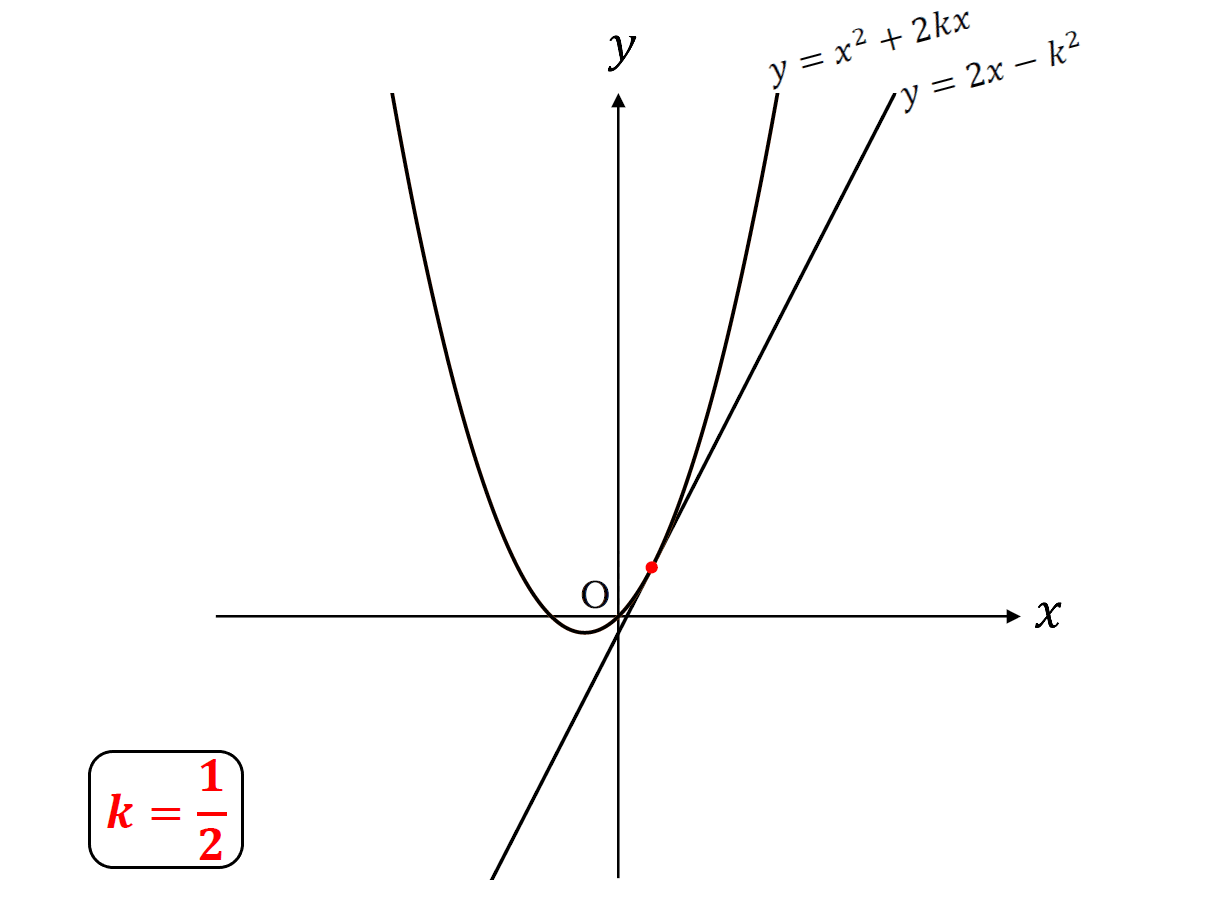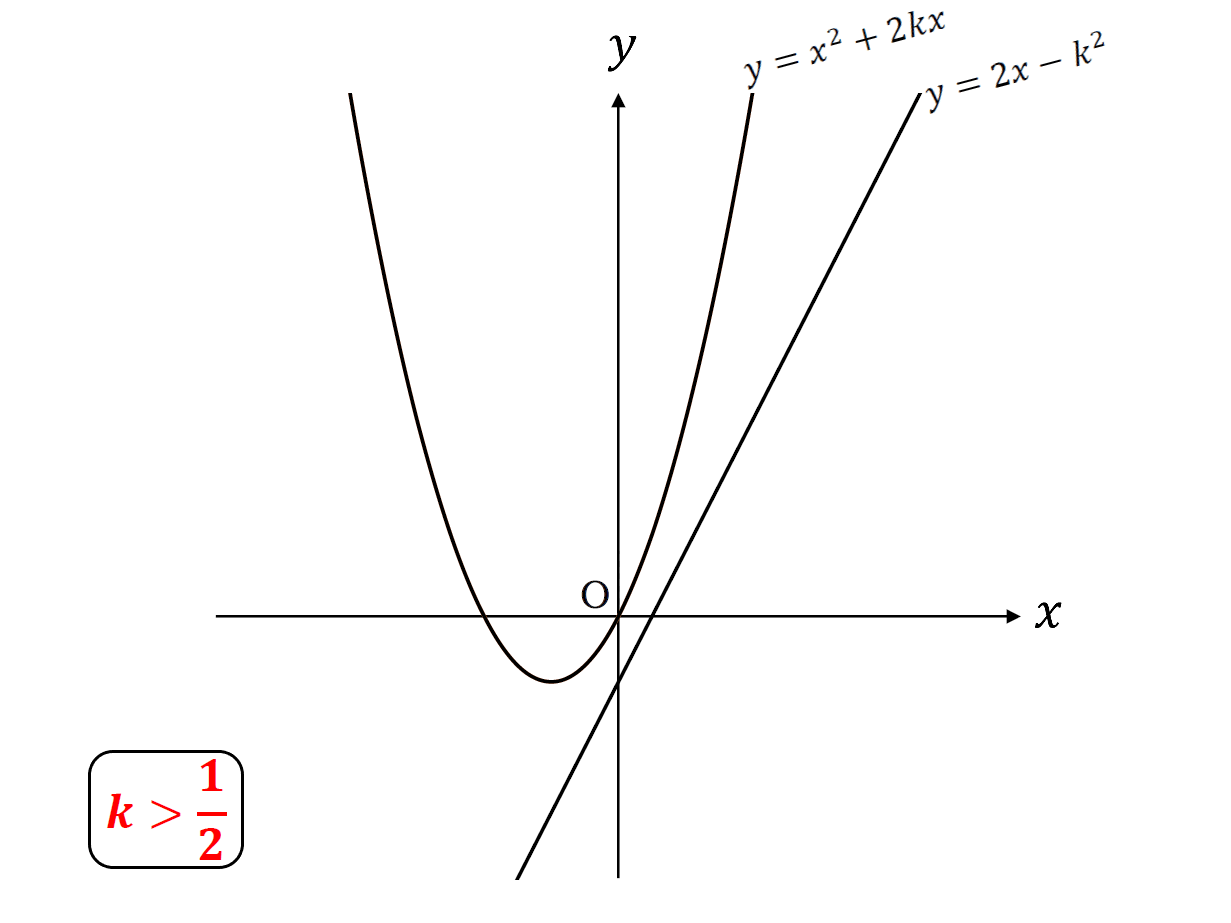
こんな感じ。
-1024x218.png)
| \(y=ax^2+bx+c\)と表し、U字の形をしている 2次関数のグラフ |
|
| \(y=mx+n\)と表し、真っ直ぐな線 1次関数のグラフ |
|
| 複数の変数を含む複数の方程式 | |
| 2つ以上の関数や図形が共通して持つ点 | |
| \(D=b^2-4ac\) |
解の公式の

ここが判別式。
 判別式の使い方
判別式の使い方
-1024x691.png)
放物線と直線の共有点を求めるとき、文字が入っているとグラフが疑似的に動く。
やることは基本的に「放物線と直線の共有点の求め方」と同じ。
違いは、計算の中に文字が入る分、整理や不等式処理が少し増えるだけ。
問題文をしっかり読み解いて、場合分けして考えることで解くことができる。
 すうがくのいえ
すうがくのいえ 

