すうがくのいえ 
2次不等式の問題を解いていると、特定の区間で2次関数が常に正または負になる条件を求める出題に出会うことがある。
いわゆる区間で定符号になる条件の問題。
「符号が同じ」「符号が変わらない」という感じ。
符号というのは、正（プラス）か負（マイナス）のどちらか。
つまり、「ずっとプラス」「ずっとマイナス」の状態を定符号という。
2次関数のグラフで見ると少しわかりやすい。
たとえば、2次関数\(y=x^2-10x+26\)のグラフは
どんな\(x\)の値をとってもプラスになることが分かる。
また、2次関数\(y=-x^2+10x-26\)のグラフは
どんな\(x\)の値をとってもマイナスになることが分かる。
𝑥軸との共有点の個数を求めることで、グラフの位置関係を調べることができる。
2次関数におけるx軸との共有点の求め方
また、絶対不等式の考え方にちょっと似ている。
【2次不等式】絶対不等式とは？常に成り立つ条件
こんな感じに、定符号とは、符号が一定ということ。
この不等式は、\(0\)≦\(x\)≦\(4\)という区間のすべての\(x\)に対して正であることが求められている。
つまり、2次関数がこの区間上で常に正である、いわゆる「区間で定符号を保つ条件」を考えなくてはならない。
区間上の符号を考えるためには、その区間における2次関数の最大値・最小値を押さえる必要がある。
区間ってなに？2次関数の最大値と最小値
また、係数に文字\(𝑎\)が入っているので、グラフそのものの位置が動くという特徴がある。なので、動くグラフとして最大・最小を考える手法も活用できる。
【2次関数】動くグラフにおける最大と最小
そして、結局は2次関数の値が正である条件を求める不等式の問題なので、2次不等式の基本的な考え方も押さえておかなきゃいけない。
2次不等式とは？グラフから理解する基本的な解き方
不等式\(x^2-2ax+a+6\)＞\(0\)の左辺をyとおくと、\(y\)＞\(0,y=x^2-2ax+a+6\)となる。2次関数\(y=x^2-2ax+a+6\)の最小値が\(0\)≦\(x\)≦\(4\)の区間で\(0\)より大きくなる条件を求めるという考え方ができる。
とりあえず、\(y=x^2-2ax+a+6\)を平方式に平方完成する。
下に凸のグラフは、区間の端と頂点のうち、軸に一番近い方が最小値になる。
なので、軸\(x=a\)が区間\(0\)≦\(x\)≦\(4\)の内か外かで場合分けをしなきゃいけない。
①\(a\)＜\(0\)のとき
②\(0\)≦\(a\)≦\(4\)のとき
③\(a\)＞\(4\)のとき
こんな感じ。
順番に考えていく。
①\(a\)＜\(0\)のとき
軸が区間の左外側の場合、軸に近い方の区間の端で最小値をとる。
\(x^2-2ax+a+6\)＞\(0\)に\(x=0\)を代入する。
これが一つ目。
②\(0\)≦\(a\)≦\(4\)のとき
軸が区間内の場合、頂点で最小値をとる。
\(x=a\)は平方完成後の\((x-a)^2-a^2+a+6\)に代入した方が解きやすい。
なので、\((x-a)^2-a^2+a+6\)＞\(0\)に\(x=a\)を代入する。
これが二つ目。
③\(a\)＞\(4\)のとき
軸が区間の右外側の場合、軸に近い方の区間の端で最小値をとる。
\(x^2-2ax+a+6\)＞\(0\)に\(x=4\)を代入する。
これが三つ目。
①\(-6\)＜\(a\)＜\(0\)または②\(0\)≦\(a\)＜\(3\)なので
①②③を並べて、区間\(0\)≦\(x\)≦\(4\)のすべての\(x\)で\(x^2-2ax+a+6\)＞\(0\)が成り立つかどうかをグラフで見てみると
\(a\)の範囲によって、区間\(0\)≦\(x\)≦\(4\)で成り立たない\(x\)が視覚的に分かる。
このグラフの動きをなんとなくでもイメージできるようになれば、思考がはかどる。
例題を解きながら、絶対不等式の特徴を確認していく。
左辺を\(y=x^2-2mx-m^2\)と置いて\(y\)≦\(0\)という条件を得る。
区間\(0≦x≦2\)で2次関数\(y=x^2-2mx-m^2\)の最大値が\(0\)以下となる条件を求めるという考え方ができる。
\(y=x^2-2mx-m^2\)を平方式に平方完成する。
下に凸のグラフは、区間の端のうち、軸から遠い方が最大値になる。
なので、軸\(x=m\)が区間の中央値\(c\)よりも小さいか大きいかで場合分けをしなきゃいけない。
区間の中央値は \[c=\frac{0+2}{2}=1\] なので、
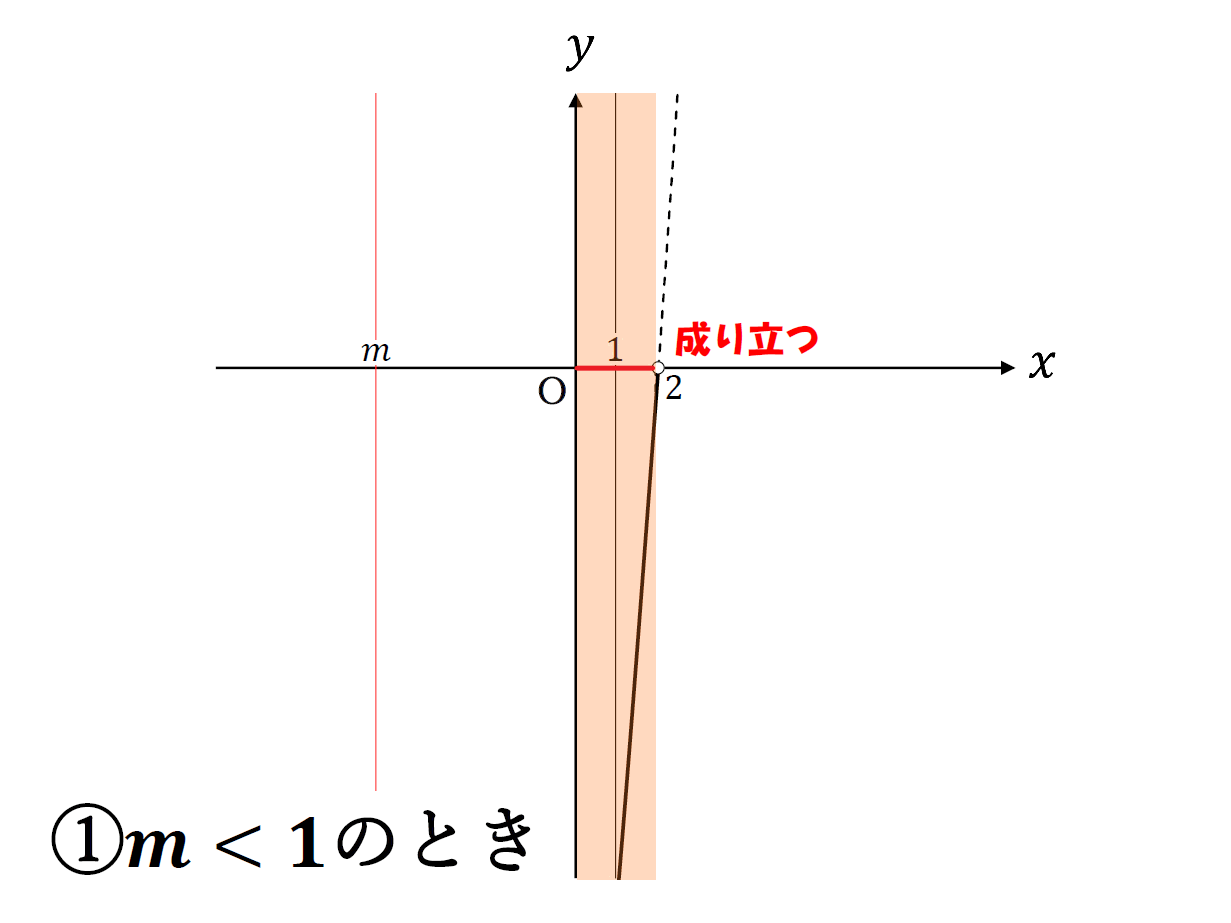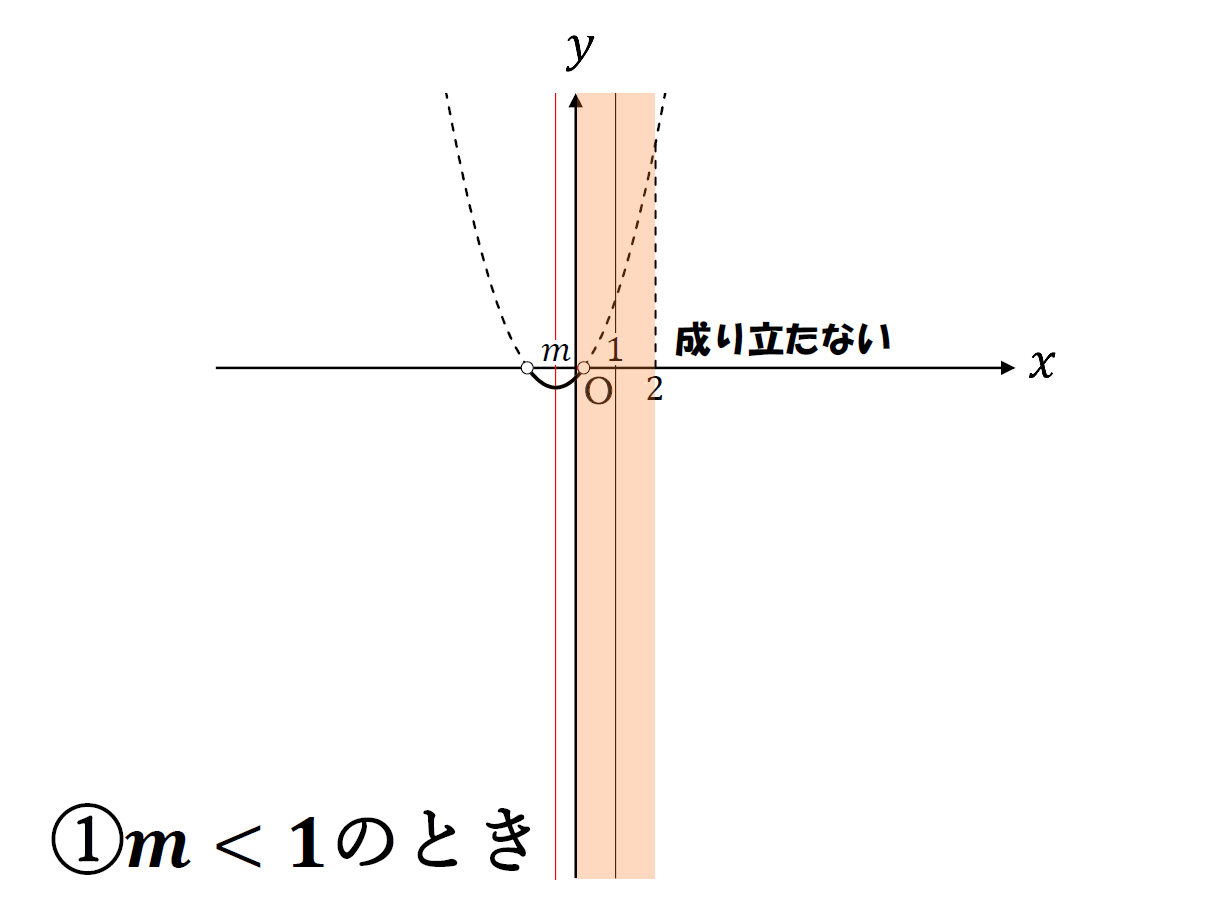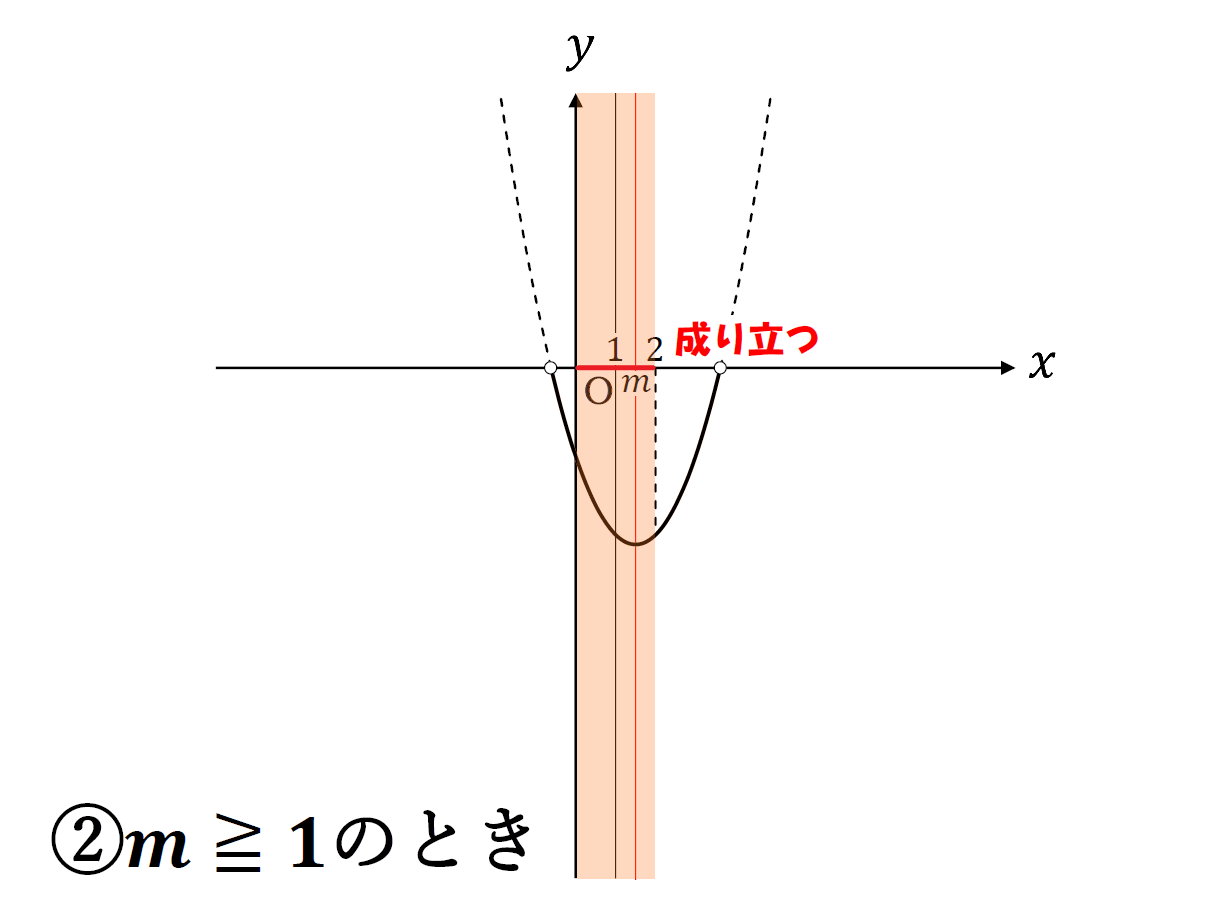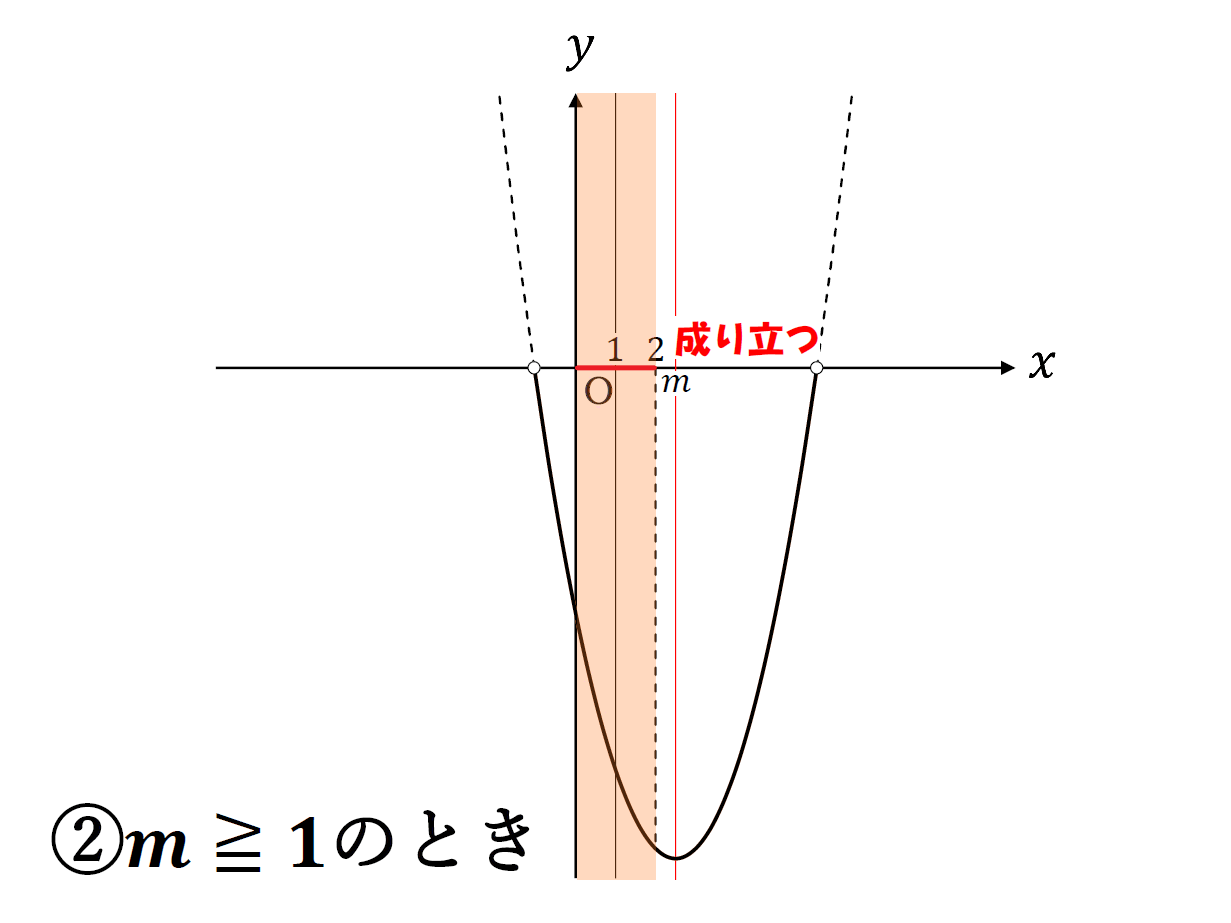
①\(m\)＜\(1\)のとき
②\(m\)≧\(1\)のとき
こんな感じの場合分けになる。
☆軸と中央値が同じとき
軸と中央値が同じとき、区間の両端とも最大値をとる。なので、「軸と中央値が同じとき」という場合分けをしないといけないように見える。今回の問いは「不等式が成り立つ範囲」を求めたいので、不等式が成り立つのであれば、「軸と中央値が同じとき」という場合分けをしなくても良い。つまり、区間の両端とも最大値をとるならば、軸が区間の中央値よりも小さいときか大きいときのどちらかに包含することができる。上記の解き方では大きい方に含んで場合分けを2つにしている。
軸が区間の中央値\(c\)よりも小さい場合、軸から遠い区間の端\(x=2\)で最大値をとる。
解の公式を使うと
②\(m\)≧\(1\)のとき
軸が区間の中央値\(c\)よりも大きい場合、軸から遠い区間の端\(x=0\)で最大値をとる。
すべての実数\(m\)かつ\(m\)≧\(1\)なので
①\(m\)≦\(-2-2\sqrt{2},-2+2\sqrt{2}\)≦\(m\)＜\(1\)または②\(m\)≧\(1\)より
①②を並べて、区間\(0\)≦\(x\)≦\(2\)のすべての\(x\)で\(x^2-2mx-m^2\)≦\(0\)が成り立つかどうかをグラフで見てみると
こんな感じ。
| 符号が一定ということ | |
|
\(ax^2+bx+c\)＞\(0\) \(ax^2+bx+c\)＜\(0\) \(ax^2+bx+c\)≧\(0\) \(ax^2+bx+c\)≦\(0\) (\(a,b,c\)は定数、\(a≠0\)) |
|
| \(a(x-p)^2+q\) | |
| 2次の多項式を平方式や完全平方式に変形させること | |
| 定義域に制限がある際の、\(x\)の値の範囲の実数\(x\)の集合のこと | |
| 区間のちょうど真ん中の値のこと |
区間で定符号になる条件は、区間における最大値・最小値の考え方や、動くグラフの最大値・最小値の考え方を取り入れなければならない。
そこから、どのような場合分けをすればいいのか、最大値や最小値はどこでとることになるのかをしっかりイメージしていきたい。
また、2次不等式を解く力もしっかいと身に付けておきたい。
