「ルート」っていう存在は知ってるけど、正直得体が知れない。
数字の周りをニョロニョロしてフタするやつ。

2乗するとaになる数を、「aの平方根」って言い方をする。
例えば、2乗すると「4」になる数は、「2」と「-2」だから、4の平方根は±2である。
実際に、±2を2乗すると4になる。
平方とは、ある数を2乗すること。
「aの平方根」は2乗すると「a」になる。
実際に数字を入れてみると、

こんな感じ。
平方根を表すのに「根号(こんごう)」という記号を使って、
根号の中に数字や文字が入っていたら「ルート」って呼ぶ。

こんな感じ。
「根号a」とは言わない。
言うとしたら「aの平方根」って感じ。
実際にルートを使ってみると、

こんな表し方になる。
根号の中の数字や文字が「正の数」「0」「負の数」のときで、
平方根の扱いが変わってくる。

「正の数の平方根」は2つある。
例えば、「4の平方根」を考えてみる。
つまり「2乗すると4になる数」を考えてみる。

こんな感じに、「2」と「-2」のプラスマイナスの2つある。
根号を使って表すと、

こんな感じになる。
他の数字でも見てみると、

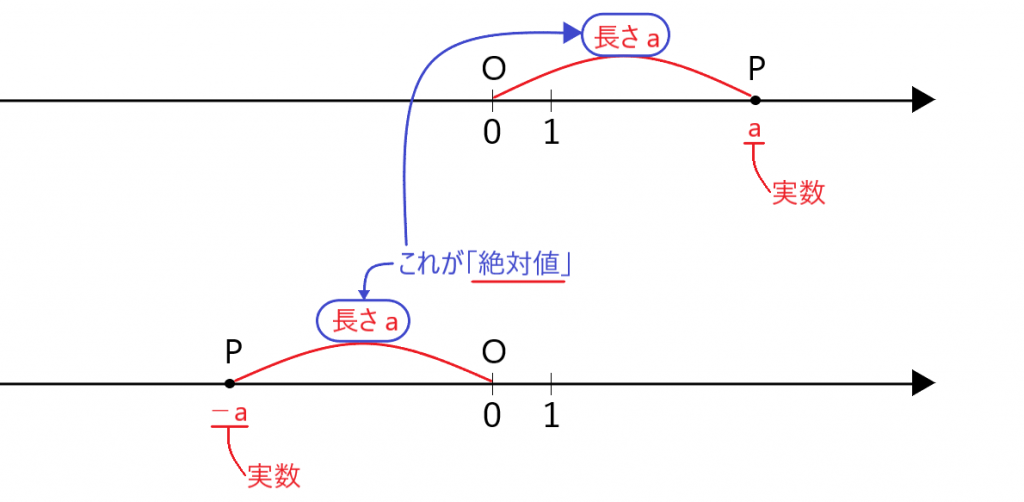
このプラスマイナスの2つの数は、絶対値が同じになるという性質がある。

つまり、数直線上で言えば、基準点Oからの距離が同じ。

0の平方根、つまり、2乗して0になる数というのは、
正の数と違い「0」の1つだけしかない。
負の数の平方根は、
実数の範囲では存在しない。
「4の平方根は±2」の場合、たまたま整数の形になったけど、
「2の平方根」とか「3の平方根」は整数の形にはならない。
とりあえず、分かりやすくするため±のうち+だけ見ていく。

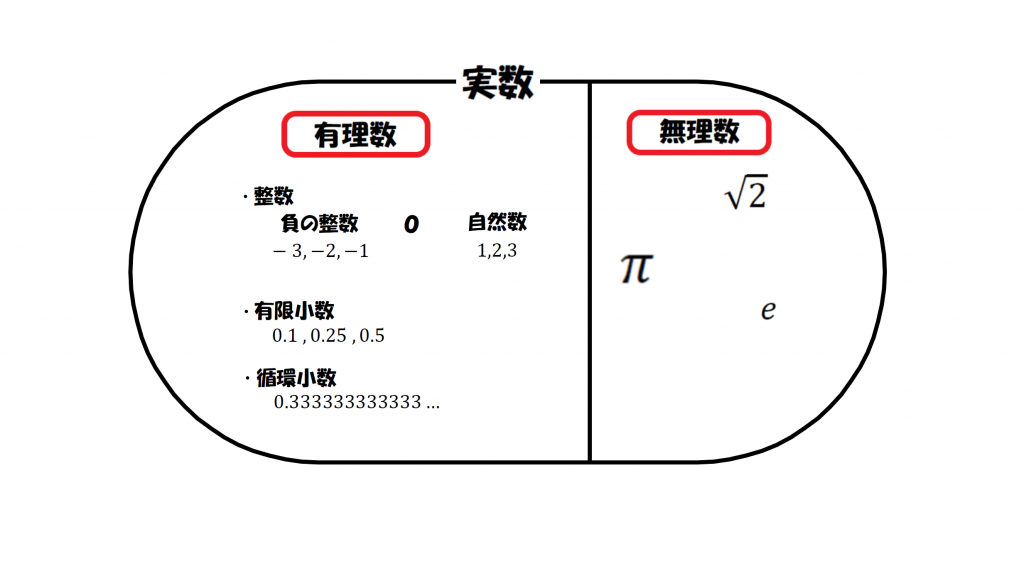
こんな感じに、終わりのない循環しない少数、無理数になる。
数字の羅列を覚えるのは難しいけど、
よく出てくる平方根の近似値は、
有名な語呂合わせがあるからそれでなんとなく覚えておけば良い。

ルート2と3と5くらい覚えておけばとりあえず良き。

「平方根」の定義が地味に分かりにくい。
ルートの計算問題を解きまくってたら感覚的に分かるようになると思う。
平方根を表す記号


平方根は、扱いが結構難しいと思う。
展開が組み立て作業で因数分解が分解作業というのと似ている。
2乗するとaになる数というのは、計算するというより、
計算された数字を巻き戻す感覚に近い。
分かりにくい。
ムズイ。
けど、いろんな式に腐るほど出てくる。
腐らないように料理しよ。
 すうがくのいえ
すうがくのいえ 


≪…2乗したらある数になる数のこと…≫は、虚数(i)も含めて、2次元から1次元のなかまいりをする数と観たい。
平面(□)を実数直線にとかしこむ≪…魔法のツール…≫である。
虚数(ー□)(i²=ー1)は、離散数直線から実数直線を手に入れる≪…魔法のツール…≫で、数直線の【0】の位置が右にずれ(進み)(-1)の(ー□)として溶け込むと観たい。
これは、絵本「みどりのとかげとあかいながしかく」の【戦い】の結果とも観えてくる。
□への纏め上げは、絵本「もろはのつるぎ」に観えそうだ・・・
≪…「ルート」っていう存在は知ってるけど、正直得体が知れない。…≫を、円環(〇)からの送りモノとして眺めると、√2 √3 は、円環の三等分 四等分の弦になる。
これから、数学の基となる自然数を大和言葉の【 ひ・ふ・み・よ・い・む・な・や・こ・と 】からの送りモノとして眺めると、[数のヴィジョン]の[コンコン物語]になるとか・・・
√ は、数を平面(2次元)からの送りモノとして眺める1次元(実数直線線分)と観える。