式を因数分解するとき、ちょっとした技を使うと因数分解しやすくなる。
因数分解とは、1つの多項式を、1次以上の多項式の積の形に変形すること。
簡単に言うと、足し算から掛け算にすること。

置き換える技は展開の技とほぼ同じ。
繰り返し出てくる式とかややこしい式を「=A」と置き換える。

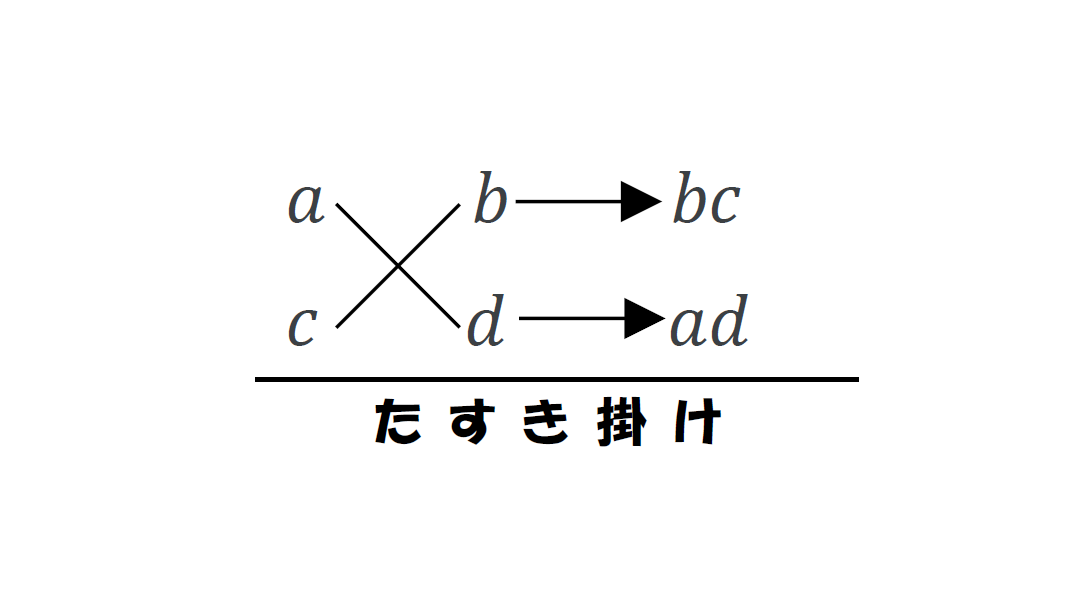
これでたすき掛けを使って解くことができる形になった。

こんな感じになるので、

とりあえず、ここまで因数分解できる。

ここで、「A」というのはこっちで勝手に置き換えた文字なので、問題に使われている文字の形に戻す。
戻したら、内側にある( )を外して簡単な形にする。

これで因数分解できた。
式を文字に置き換えて公式が使える形や、たすき掛けができる形にすると、
難しそうなややこしい因数分解でも解くことができる。

いくつかの文字が同時に出てくるややこしい問題も出てくる。
そういう時は、「一つの文字について整理する」技を使うと、
上手く因数分解できる。
あーもう文字だらけヤバい無理。
ってなるけど、一つずつ見ていくとちゃんと解けるようになっている。
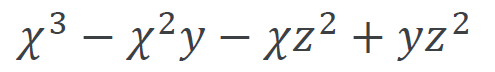
何故、次数が一番低い文字について整理するのかというと、
次数が低い式ほど、扱いやすいから。
4乗だと定数項も含めて5つの項、3乗だと4つの項、2乗だと3つの項、
という感じに、次数が減るごとに項が減って考えるべき選択肢を減らすことができる。
その方が計算楽。
もし、次数が同じ文字しかない場合は、係数が小さい文字に注目する。
次数っていうのは、掛け合わせた文字の個数(文字の指数の和)のこと。
で、ここで見るのは多項式の次数。
多項式の次数は、同類項をまとめて整理した多項式において、各項の次数のうち、最も次数の高い項の次数。
つまり、ここではそれぞれの文字について、一番高い次数は何なのかをまず見ていく。

こんな感じ。
ここで、今度は文字を比べて、次数が一番低い文字に注目する。
この場合だと、「y」が一番次数が低い。
なので、ここで「y」について式を整理していく。
整理の仕方は「降べきの順に整理」をする。
降べきの順に整理とは、項の次数の高い方から順に並べること。

こんな感じに整理する。

整理出来たら、とりあえず共通因数でくくっていく。
また共通因数があるのでくくる。

ここで、因数分解の公式に当てはまる式があるので、公式を使う。

これで因数分解できた。

技の種類とそのステップ。

単純に公式だけ覚えていれば、因数分解ができるわけではない。
やっぱり計算には技とかコツがいろいろある。
かといって公式を覚えていなければ、時間がかかってしょうがない。
さらに、因数分解の公式を覚える前提として、展開の公式を覚えておいた方が良い。
その展開の公式を覚える前にも何故そんな公式になるのかを知っておけばもっと楽になる。
こんな感じに、数学は積み重ねの教科だと言われるのはその通りで、
逆に、一つずつ確実に積み重ねていけば確実に問題を解くことができる。
費やした時間が多ければ多いほど、確実に身に付く。
 すうがくのいえ
すうがくのいえ 
.png)