一難去ってまた一難。
強敵その壱に続いて、解けない問題。
コイツもあらかじめ知っていないと、初見では進めないだろってヤツ。
解答を見たらそうなるんだろうとは思うけど、
解法を知らないまま導出していくのは難しいんじゃないかと思う。
その弐

この式を因数分解する。
3乗はムズカシーネー。
ついマイナスでくくっちゃって、
ソッコー身動きが取れなくなってペンを置いた。
3乗の展開はどうせしないだろう。
という、先入観から抜け出せなかった。
まず、(a+b)=Aと置き換える。

ここで、
展開。

展開しちゃうんかい。
展開しちゃうとは思わなかった。
ぐちゃぐちゃになりそうだけど、ここでAの3乗のみに注目。

3乗だけに注目してさらに展開しちゃう。
これは思いつかん。
ところどころ「A」を残して、指数が3乗の文字たちを相殺する。

ここで共通因数「3」でくくる。

さらに( )の中を共通因数「ab」「Ac」でそれぞれくくる。

こ・こ・で!!
ようやくここで!
「A」を元の形に戻す。
そうだ忘れてた。
置き換えてたんだった。
Aが置き換えた文字ってこと忘れてた。

おかえり。
汝のあるべき姿に戻った。
おかげで共通因数(a+b)をくくることができる。

結構分解出来てきた。
けど、ここで{ }の中を展開して「cについて降べきの順に整理」する。
展開と分解が目まぐるしい。

これで因数分解の公式3.を使うことができる。

こんな感じになって、一応終わり。
これでも正解。
正解なんだけど、欲を言うとキレイに整理したいから、「輪環の順」を使っちゃう。

綺麗な形にしたらこんな式になる。
これでも正解。
これで因数分解できた。
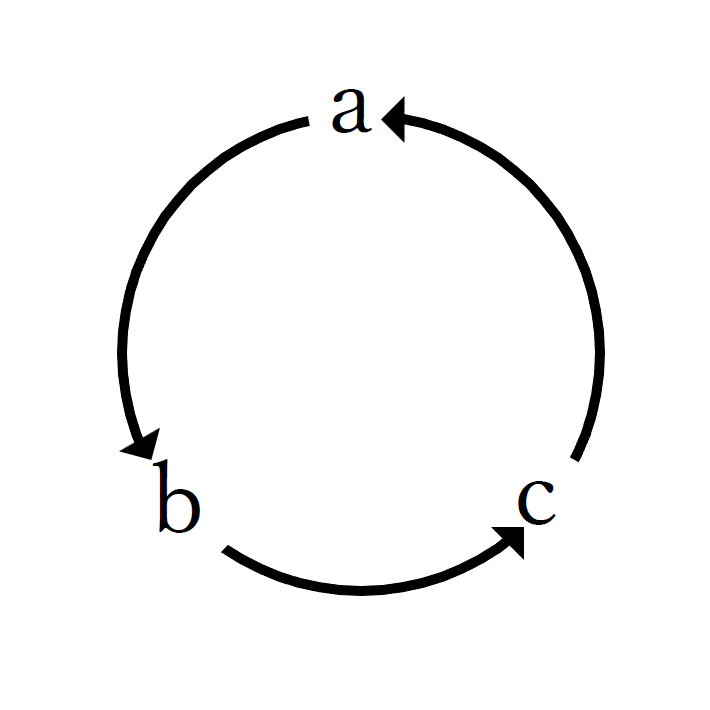
| 輪環の順 (りんかんのじゅん) | a→b→c→a→…という、 循環することを意識した式の書き方 |
| 降べきの順に整理 | 項の次数の高い方から順に並べること 高いところから低いところへ降りていくイメージ |
| 昇べきの順に整理 | 項の次数の低い方から順に並べること 低いところから高いところへ昇っていくイメージ |
| 特定の文字に着目 | ・2種類以上の文字を含む単項式において、着目する 文字によって、式の次数、係数が変わる。 ・着目する文字は一つとは限らない。 ・着目した文字以外の文字は単なる数と考える。 |
知っておかなければならないわけではないが、知っておくと問題を解きやすくなる。
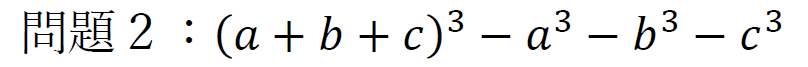
解き方が分かった上でもう一度何も見ずに解いてみると結構身に付く。
初見では解けないだろっていう問題はいくつもある。
解答を見たらそうなるんだろうとは思うけど、
解法を知らないまま導出していくのは難しい問題。
今回の強敵を必ず解けなければいけないというわけではないけど、
強敵の倒し方を知っておけば、また別の強敵を倒すのに役に立つことがある。
その時に備えて解き方を覚えておいても損はないのではないんじゃないかと思う。
公式として問題と答えだけ覚えておくのもアリっちゃアリ。
カレー食べた。
 すうがくのいえ
すうがくのいえ .png)
.png)
