実数の中でも、有理数であればどんな数字でも分数の形にすることができる。
どうやって分数の形にするのかを確認していく。
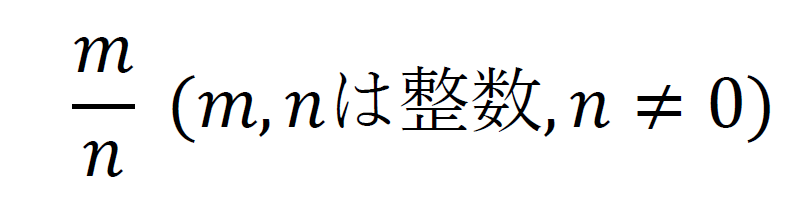
あらかじめ有理数が何なのかを確認しておく。
有理数は、
・整数
・有限小数
・循環小数
の3種類。
一つずつそれぞれ分数の形にしていってみよう。

こういうのが整数。
整数とは、0と、0に次々1を足した数と、0から次々1を引いた数で、少数のない数。
分数で表すならば、分母が「1」ということになる。
ということを踏まえて、分数で表すと、

こんな感じになる。
これで整数を分数にできた。

こういうのが有限小数。
有限小数とは、終わりのある少数のこと。
有限小数は、まず小数第何位まで数字があるかを見る。
それを整数にするために、10や100を掛けていく。
その掛けた10や100は掛けただけ分母に表す。

こんな感じになる。
これで有限小数も分数にできた。

問題はこの人たち、循環小数。
有理数の中で一番分数にしにくいやつ。
循環小数とは、終わりのない循環する少数のこと。
有限小数に対して無限小数とも呼ぶ。
表し方の特徴として循環する部分の数字の始めと終わりの上に「・」をつけて表す。
これ全部分数で表せます。
具体的に考えていこう。

同じ数字が永遠と続く循環小数を分数で表してみる。

なんでもいいので、とりあえず「=A」と置き換える。

次に、両辺を10倍する。

こんな感じになる。
これで例1は分数で表すことができた。

今度は、2つの数字が永遠と続く循環小数を分数で表してみる。

なんでもいいので、とりあえず「=A」と置き換える。

次に、両辺を100倍する。

こんな感じになる。
これで例2も分数で表すことができた。

今度は、3つの数字が永遠と続く循環小数を分数で表してみる。

なんでもいいので、とりあえず「=A」と置き換える。

次に、両辺を10000倍する。

まず小数点以下を揃うようにする。
小数点以下が揃ったら引き算をする。

こんな感じになる。
これで例3も分数で表すことができて、循環小数を分数にできた。

一番厄介な循環小数を分数にするステップ。
STEP1.文字に置き換える
STEP2.循環部分を整数部分まで来るようする
STEP3.小数点以下が揃うようにして引き算する
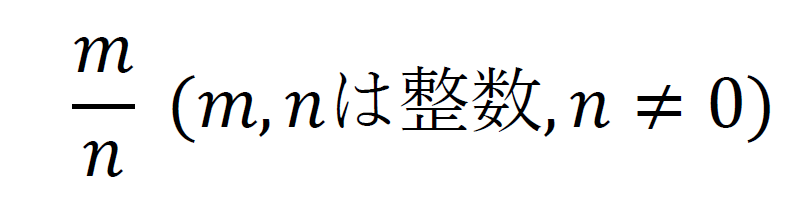
手順さえ覚えておけば、どんな有理数も分数にできる。
 すうがくのいえ
すうがくのいえ 

