多項式って言われても正直ピンと来ない。
「ん?タコーシキ?…え?」ってなる。
多項式って一体何なのだろう。

結論から言うと多項式っていうのは上みたいな感じの式。
多項式が一体何なのかを知るためにはまず「単項式」っていうのを知らなくてはいけない。
「単項式」の正体を暴くと「多項式」が何者なのか分かる。
「単項式」とは、
数や文字だけの積の形で表された式。
つまり、数字と文字の掛け算の形。
「多項式」とは、
単項式の和として表される式。
つまり、単項式の足し算の形。


式で表すとこんな感じ↑。
単項式は数字と文字の掛け算なので、多項式は掛け算の足し算ともいえる。

多項式は掛け算の足し算ということが分かった。
分数やルートが入っていると多項式とは呼ばないらしい。


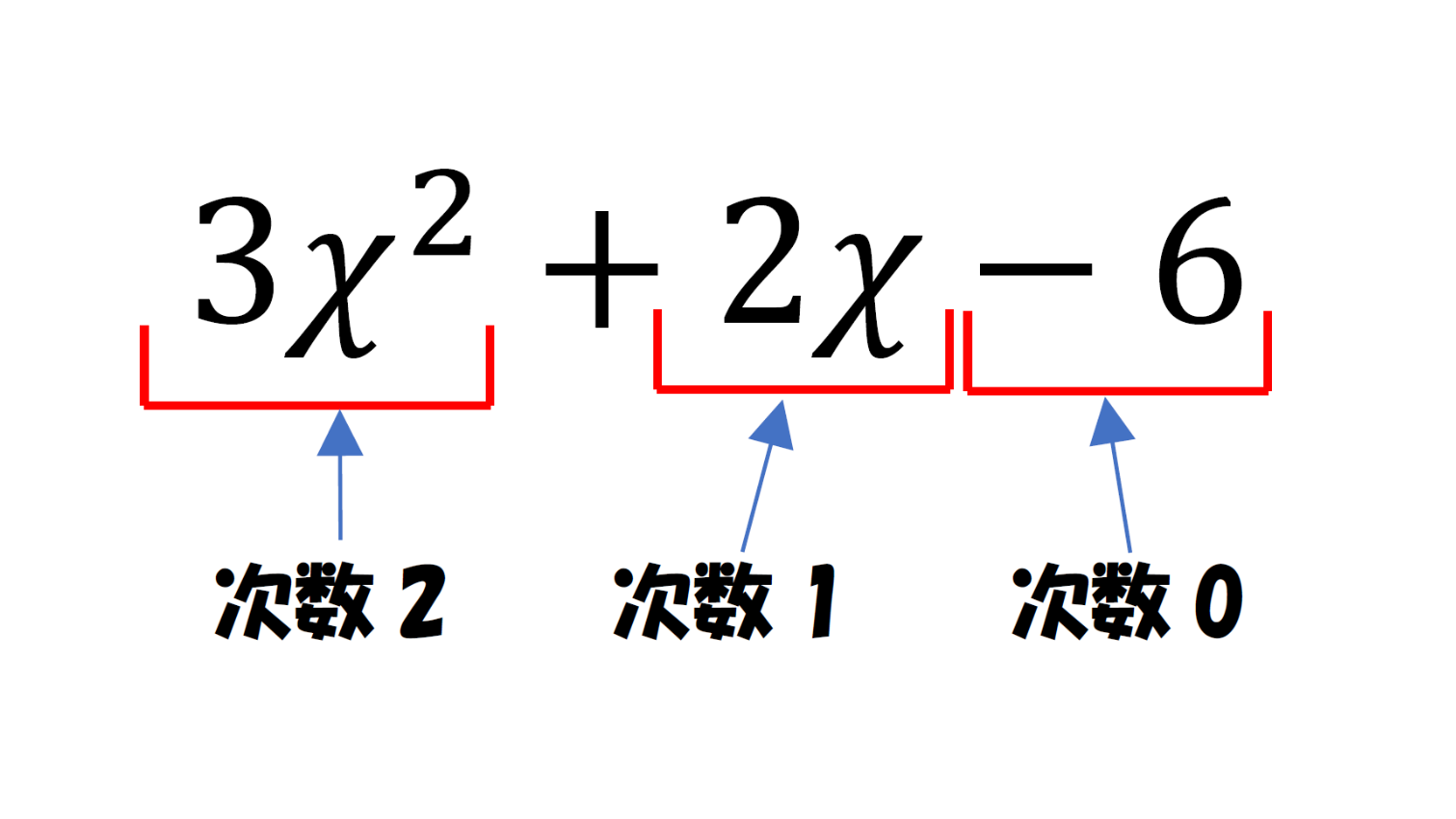
もう少し細かく中身を見ていくと、単項式において、その文字に係る数の部分を「係数」、数や文字の右肩に付記して、その累乗を示す数字や文字を「指数」と呼ぶ。
「累乗」っていうのは、同じ数を順次に掛け合わせることで、掛け合わせた文字の個数を「次数」(文字の指数の和)と呼ぶ。
そして、多項式の中の各単項式を「項」って呼ぶ。
言葉だけで説明するときに困らないよう、それぞれ名札がつけられて、そう呼ばれてるみたい。
これが「定義」というもの。
教科書を見ても何が書いてあるか分からないという状況がよくある。
そのときは、まず定義を知るところから始めれば、少しずつ何が書いてあるのかを理解することができるようになる。

多項式の事を「整式」と呼ぶこともある。この「整式」というのは、同類項をまとめた後の式のことをいう。
同類項とは、多項式の項の中で文字の部分が同じ項のこと。この同類項は一つにまとめて整理することができる。
つまり、

こんな感じ。
ここで注意すべきことが、同じ指数の文字同士をまとめること。
ってことは、

左辺は多項式ではあるが整式ではない、右辺は多項式であり整式である。
こういうことなんだと思う。
| 単項式 | 数や文字だけの積の形で表された式 |
| 多項式(整式) | 単項式の和として表される式 |
| 項 | 多項式の中の各単項式 |
| 同類項 | 多項式の項の中で、文字の部分が同じである項 |
| 係数 | 単項式において、その数の部分 |
| 次数 | 掛け合わせた文字の個数(文字の指数の和) |
| 指数 | 数や文字の右肩に付記して、その累乗を示す数字や文字 |
| 累乗 | 同じ数を順次に掛け合わせること |
今までの単語を文字で書くとこんな感じになる。
文字で書くとどうしても難しくなってしまいがちだけど、
勉強において定義を知ることは何を差し置いても大事なこと。
定義が分かっていれば教科書とか参考書を読むのも苦じゃなくなってくる。

この形の式のことを多項式と呼ぶ。要は、 掛け算と足し算で表された式のこと。
あと、同類項の整理。

これも大事。
 すうがくのいえ
すうがくのいえ