ルートの中の数字が大きいとき、もっと簡単な形にできるのであれば簡単な形のルートにしたい。
素因数分解をして、2乗になった素数をルートの外に出すことで、ルートを簡単な形にすることができる。
この2乗になった素数は平方数と呼ばれる。
平方数とは、簡単に言うと有理数の2乗のこと。
この素数の平方数を見つけられるかどうかで、ルートを簡単な形に表せるかどうかが決まる。
でも、ルートの中の数字が何の2乗なのか分からないことがある。
そんなとき、素数の平方数の見つけ方というのがある。
それが「筆算の開平法」と呼ばれるもの。
ルートを簡単な形にする方法はいくつかある
そのうち、筆算の開平法のやり方を紹介する。

平方根の具体的な数を求める計算のことを開平という。
いろいろな開平の計算方法があって、
その計算方法のことを開平法という。
いろんな開平法の中で、
視覚的に分かりやすく、効率良く計算できるやり方を「筆算の開平法」と呼ぶ。

具体的に数字を入れて考えてみる。
①小数点の位置を基準にして、2桁ずつ区切る。

②一番高い桁の区分にある「6」に注目し、6以下で6に一番近い平方数を見つけて、注目した桁の区分の上と、左のスペースに立てる。
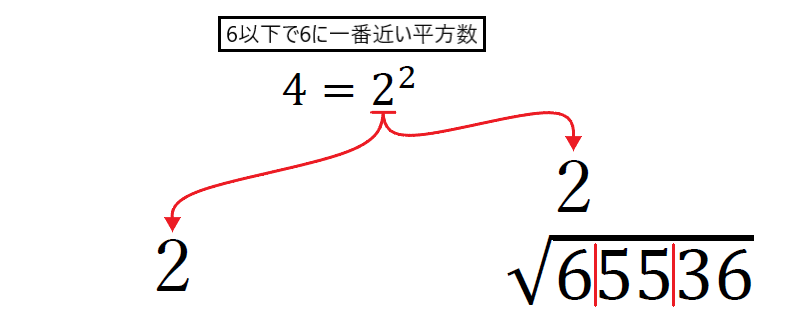
③左側と右側の数で掛け算をし、右側の注目した桁の下に4を書き、引き算をして、2番目に高い桁の区分の数を下ろす。
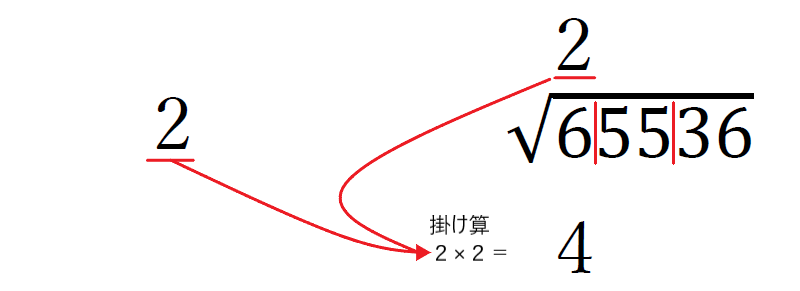
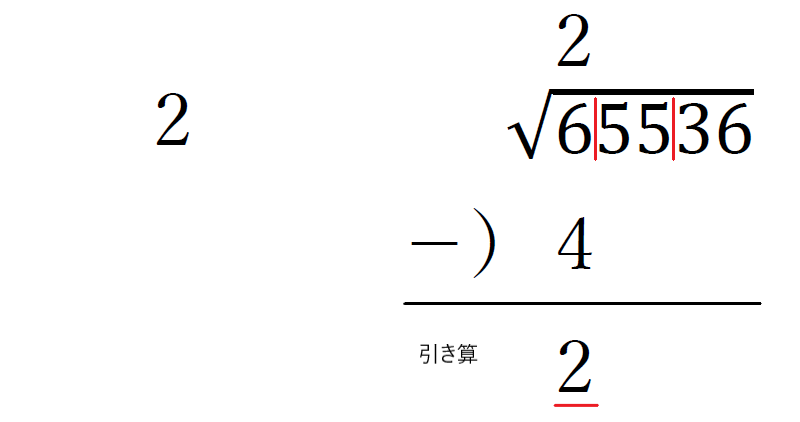
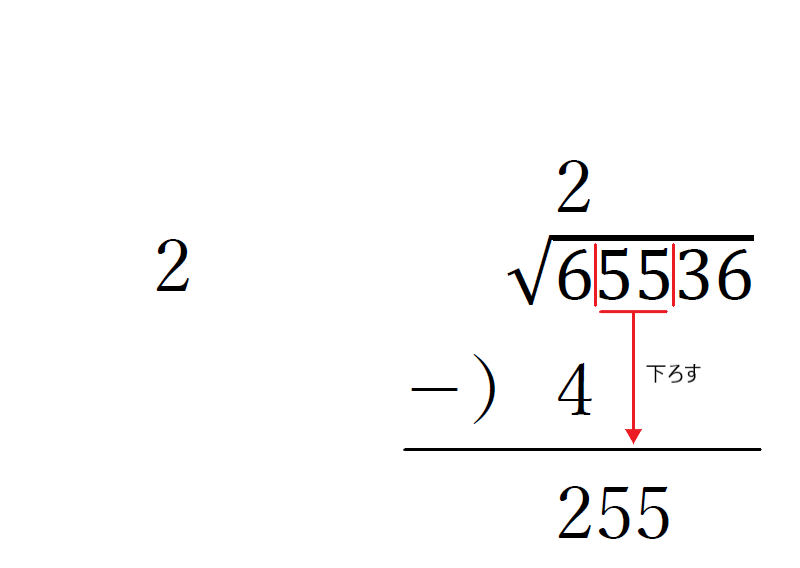
④ルートの上に立てた数を、左のスペースにも書き、足し算をする。

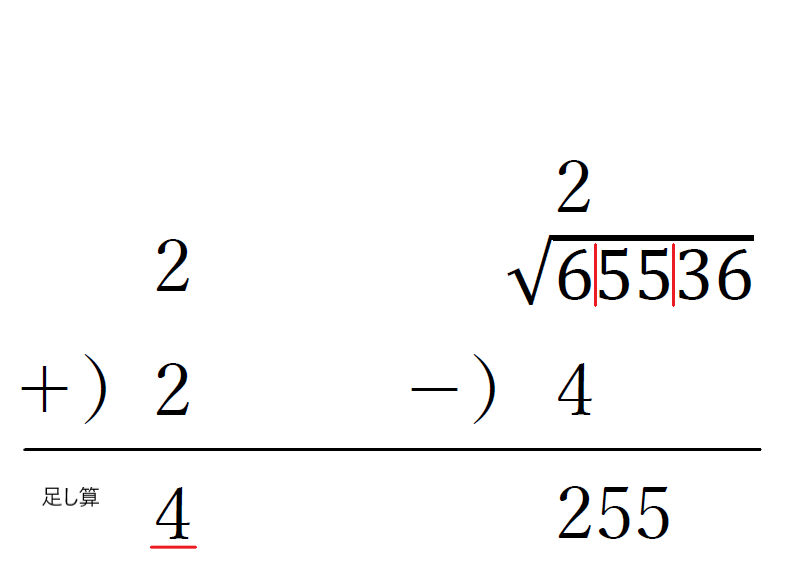
⑤左側の一の位を「N」と置き、(40+N)×Nが255以下で255に一番近くなる「N」を見つけて、二つ目の桁の区分の上と、左のスペースに立てる。

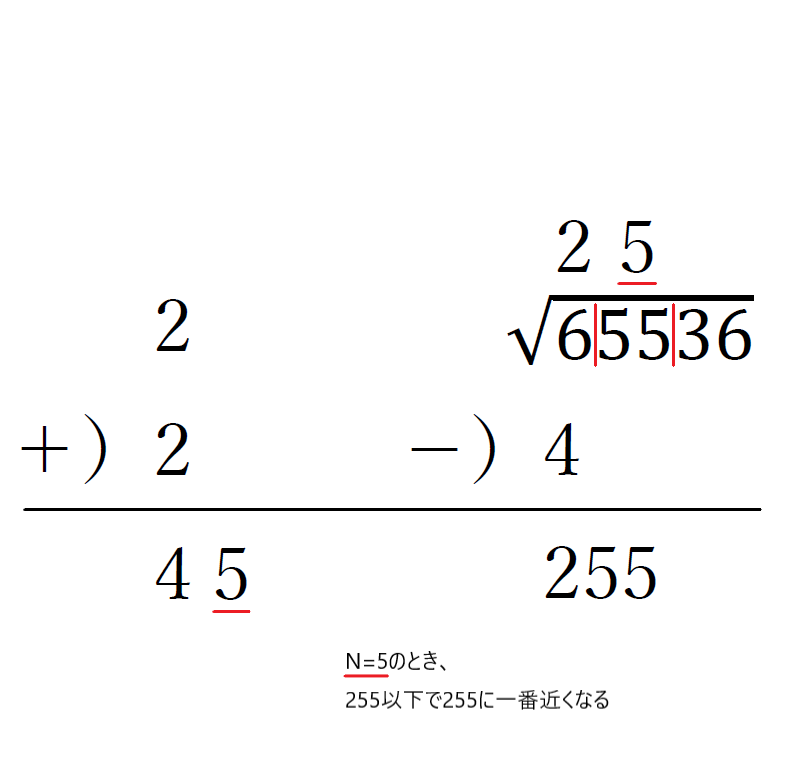
⑥左側と右側の数で掛け算をし、255の下に225を書き、引き算をして、一番低い桁の区分の数を下ろす。


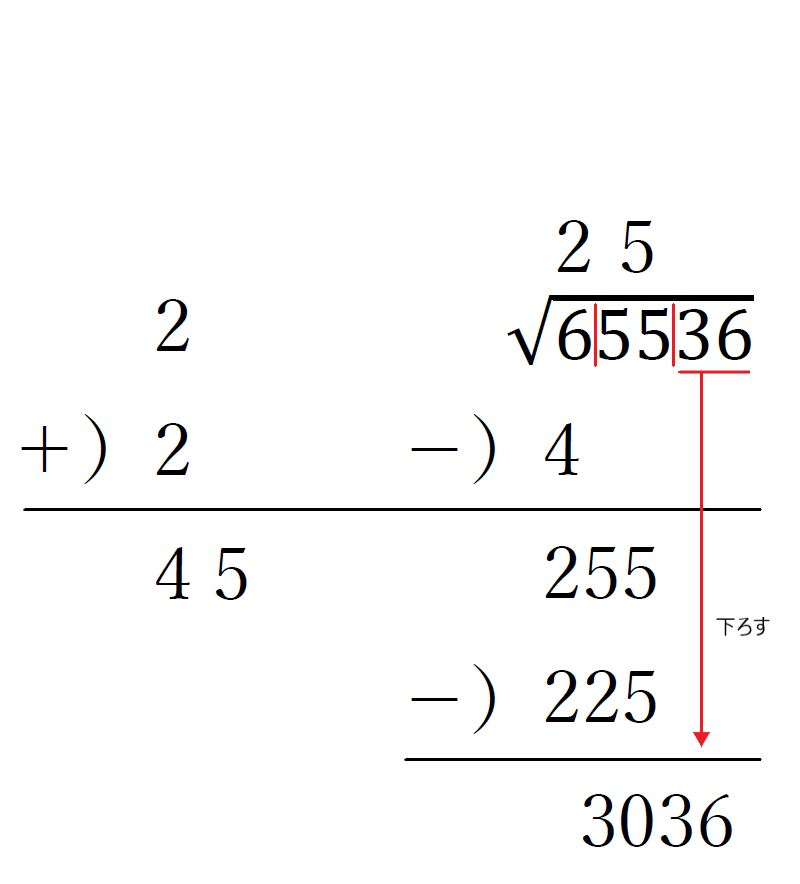
⑦ルートの上に立てた数を、左のスペースにも書き、足し算をする。


⑧左側の一の位を「N」と置き、(50+N)×Nが3036以下で3036に一番近くなる「N」を見つけて、一番低い桁の区分の上と、左のスペースに立てる。



計算結果が「0」になったので、ここで終わり。
ルートの上に書いた3桁の数が開平した数になる。

これが筆算の開平法。
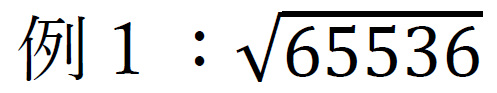
筆算の開平法にはちゃんとした原理がある。
まず、ルートを外した時に、何桁の数字になるかを調べる。
ルートの中の数について、

ということができるので、3桁であることが分かる。
3桁なので、一の位、十の位、百の位の数字をそれぞれ文字で表す。

そしてこれらを式で表すと、
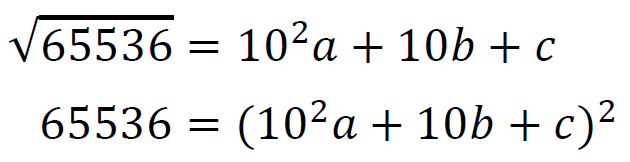
こんな感じに表すことができる。
右辺をある程度まで展開する。

こんな感じになる。
まだ展開できるけど、ここで止めておく。
筆算の開平法で、小数点の位置から2桁ずつ区切るのは、
平方根の各位が2桁ごとに立つからということが分かる。
ここで展開した式に注目すると、

こんな感じに、まず百の位が求まる。
次に、
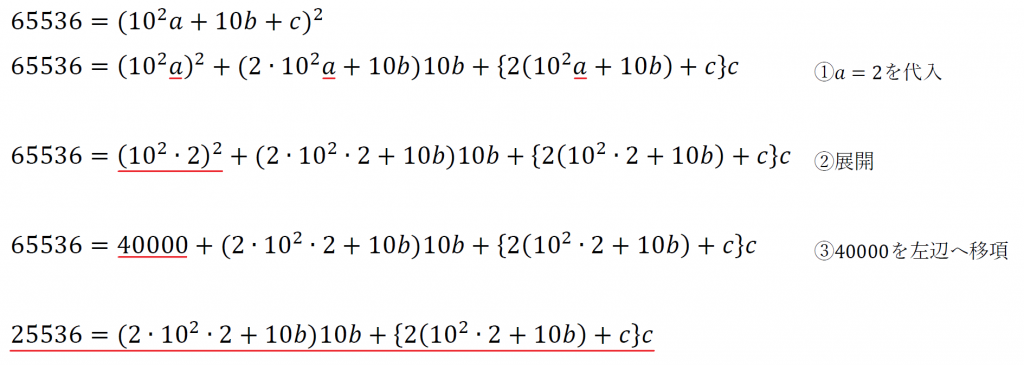
ここまで計算できる。
右辺に注目すると、

こんな感じに、十の位も求まる。
最後に、

ここまで計算できる。
右辺に注目すると、

こんな感じに、一の位も求まる。
これで3桁全部求めることができた。

これが筆算の開平法の原理。
原理を知っておくことはとても大切なこと。
今自分が何をしているのかを把握するためにも。
| 平方数 | 有理数の2乗 |
| 開平 | 平方根の具体的な数を求める計算のこと |
| 開平法 | 開平の計算方法のこと |
| 筆算の開平法 | 視覚的に分かりやすく、効率良く計算できる開平の計算方法 |
なかなか聞き慣れない言葉ばかり。
小数点を基準にするから、小数点以下にも数字がある場合にも対応できる。
使いこなせるようになるまで、何回も計算して慣れていかないといけない。
「開平法」を一つだけでも知っておけば超便利。
 すうがくのいえ
すうがくのいえ 

