問題の中には、見たことのない形の式が出てきたりする。
特殊な形の式は、順番に計算していくよりも、ちょっと変形するだけで簡単に計算することができる。
取っ付きにくい見た目でも、必ずどこかに答えまでの道が隠されている。
一度答えまでの道を見つけてしまえば楽に答えまでたどり着くことができる。
そして一度解法を覚えてしまえば、似たような問題が出てきたときでも素早く解答を導き出すことができる。
今回はそんな特殊な形の式のうち、分数の混ざったものを用意したのでそれぞれ順番に確認していこう。

まずは問題文を見てみると…
どうやって代入するんだ…
ってなる。
与式を変形してみたり問題を変形してみたりしても、なかなか答えが出そうにない。
実はこの式の形は対称式の形になっているから、
基本対称式が分かれば解けるようになっている。
といっても、今回は基本対称式がどうとかはあまり考えなくても良い。
問題文の中の式にまずは注目していけば解けるようになっている。
順番に見ていこう。
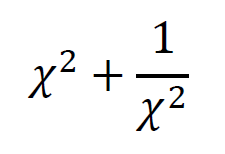
(1)の式から導くのではなく、その前の与式を変形するところから解いていく。

これで(1)の式の値を求めることができた。
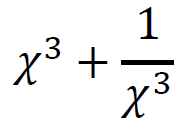
(2)も同じように、与式を変形するところから解いていく。

これで(2)の式の値を求めることができた。
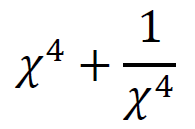
この式は、(1)の答えから導き出していく。

これで(3)の式の値を求めることができた。
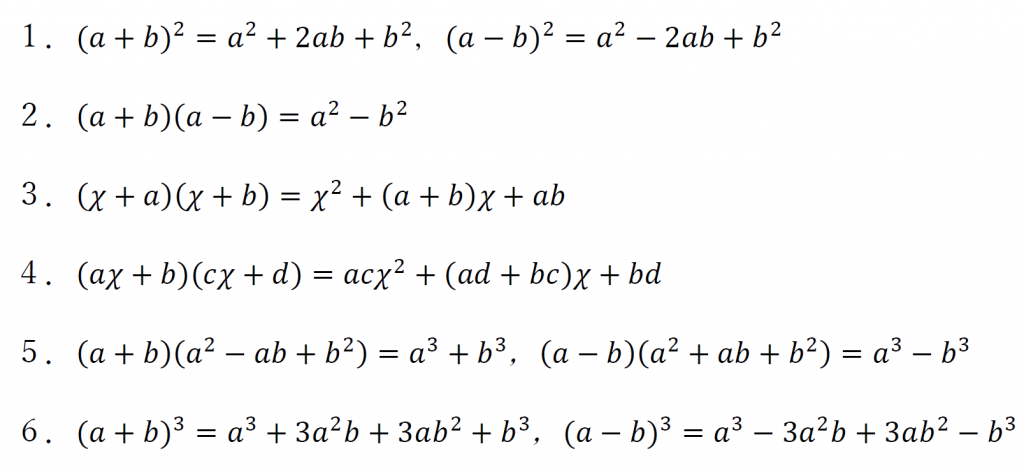
展開の公式は上のとおり。
展開の公式を覚えていれば、似たような形の式に変形できるというひらめきに繋がる。
覚えていなければ今回の問題を解くのは難しいかも。
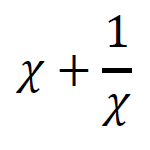
この形の式の問題は、与式を変形させていくことによって、具体的な数値を求めることができるようになっている。
問題の式ではなく、与式を変形させるのでちょっと特殊な問題だった。
それに気づくことができれば、初見でも解くことができる。
解法を知っていれば、戸惑うことなく与式の変形によって解答を素早く導き出すことができる。
そして解き方は一通りではない。
どんな問題も、たくさんの解き方があって、その中に「解きやすい」解き方がある。
そのたくさんの解き方は全て一つの答えに繋がる。
つまり、必ずしも解きやすい解き方でなくても、解き方が間違えてさえいなければ答えは出せる。
ここが数学の面白いところでもある。
選択肢は多い方が最短ルートを見つけやすい。
だからと言って最短ルートでなければならないというわけではない。
あくまでゴールが何なのか見失わないようにしなければならない。
 すうがくのいえ
すうがくのいえ