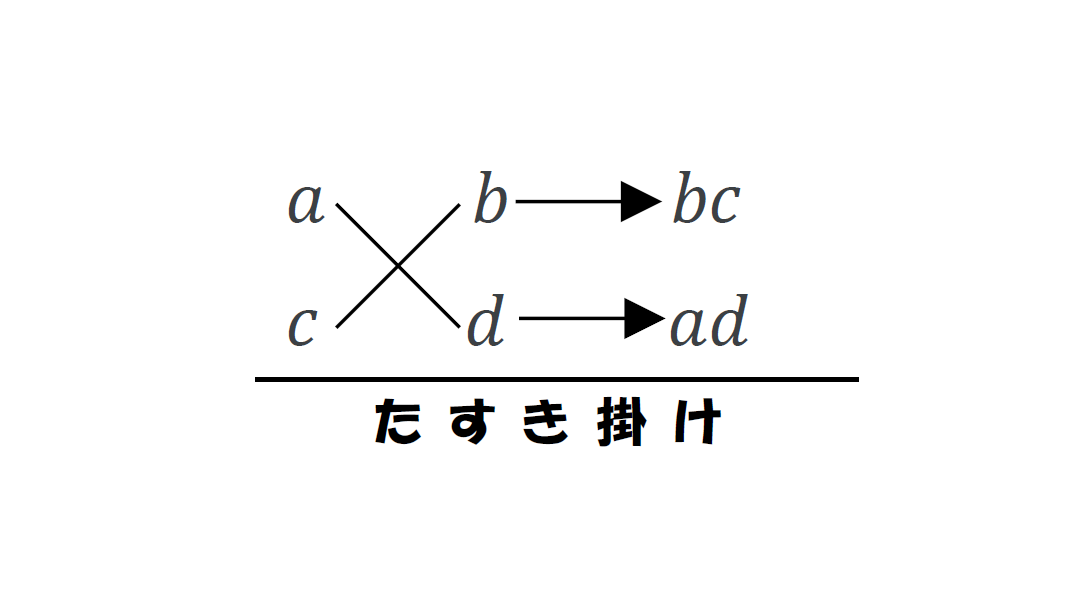
因数分解の中で「たすき掛け」という技がある。

襷(たすき)って聞くと、駅伝とか選挙の演説っぽい。
でも語源は、紐とか布地のものを使って、和服の袖をたくし上げる「たすき掛け」からきているらしい。
その「たすき掛け」をすると、両肩から両脇へ斜め十文字にかけて紐とか布地のものが結ばれる。
因数分解で使う図式が、その十文字(たすき掛け)と同じ形になっているから、
因数分解で使う図式を「たすき掛け」と呼ぶようになった。
.png)
ということで、
和服の袖のまとめ方!
ではなく、因数分解における「たすき掛け」という技をやっていこうと思う。
「たすき掛け」というのは一つの技に過ぎない。
どういうものなのかというと、

こんな感じの図式で、
因数分解の公式4.

これを使いやすくするもの。
実際に数字を入れて解いてみると分かりやすいと思う。

試しにこの式をたすき掛けで解いていく。

「6」の掛け算の組み合わせはこの2つ。
ここでは、2次の係数は、正の数の組み合わせだけ考えれば良い。

「-6」の掛け算の組み合わせはこの4つ。

まず、「xの2乗」の係数の組み合わせひとつを縦に並べる。
その右横に、「定数項」の係数の組み合わせひとつを縦に並べる。

次に、斜めに掛け算をして、結果を右へ書く。

同じようにもう片方もやる。

このバッテン部分がたすき掛けの所以。
この一番右の数字を縦に足し算して、その答えが(ad+bc)部分になる。

とりあえず足し算すると、

こんな感じになる。
他の組み合わせも試してみる。
ここで、

こんな感じの、横に並んだ数字が「1以外の公約数を持つような場合」は考えなくていい。
1以外の同じ数字になってたり、倍数になってたり。
この例で、もしこのまま式に直したとき、

こんな感じに「2,3,6でくくる」ことができてしまう。
因数分解をする前の

この式は「2,3,6でくくる」ことはできない。
2,3,6でくくることができない以上、

この組み合わせは考えなくていい。
それを踏まえて、他の組み合わせを考えると、

この4つになる。
この中で、ac+bd=-5になるのは③なので、

これでたすき掛けの図式を使って、因数分解できた。
STEP1.「xの2乗」の係数の掛け算の組み合わせ(a,c)を探す
STEP2.定数項の掛け算の組み合わせ(b,d)を探す
STEP3.これらの組み合わせの中からac+bd=-5になるものを見つける
この3つのステップで、たすき掛けの図式を使って因数分解をすることができる。

たすき掛けを覚える中にも知っておくべき定義がある。
知っておかなくてもいい豆知識もある。
| たすき掛けの由来 | 和服の袖をたくし上げるために、両肩から両脇へ斜め十文字にかけて紐を結ぶ「たすき掛け」が由来 |
| 公約数 | 2つ以上の自然数について、そのいずれの約数にもなることができる整数のこと |
| 約数 | ある整数や整式を割り切ることのできる整数や整式のこと |


STEP1.「xの2乗」の係数の掛け算の組み合わせ(a,c)を探す
STEP2.定数項の掛け算の組み合わせ(b,d)を探す
STEP3.これらの組み合わせの中からac+bd=-5になるものを見つける
たすき掛けをする前に、くくれる文字があったらあらかじめくくっておく。
たすき掛けをするのが難しい式で、無理に時間を割いてたすき掛けで解くより、「解の公式」を使った方が良い。
あくまで、たすき掛けは図式を使った一つの技に過ぎない。
 すうがくのいえ
すうがくのいえ