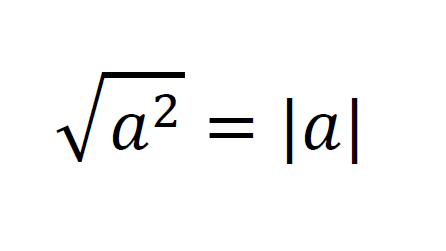ルートの中が「文字の2乗」「式の2乗」のとき、単純にルートを外すことはできない。
例えば、
\(\sqrt{a^2}=a\)
という感じに、単純にルートを外して計算したくなる。
だけど、後に\(a=-3\)ということが判明した場合、
\(\sqrt{(-3)^2}=-3\)
と計算したということになる。
正しくは、
\(\sqrt{(-3)^2}=3\)
としなきゃいけない。
つまり、先程の計算は間違っていることになる。
なので、ルートの中が「文字の2乗」「式の2乗」のとき、単純にルートを外してしまうと、間違った計算をしたことになる。

まずはルートの性質、つまり平方根の性質を確認する。
2乗すると\(a\)になる数を、「\(a\)の平方根」と呼ぶ。
文字通り「\(a\)の平方根」を2乗すると\(a\)になる。
\((a\)の平方根\()^2=a\)
2乗すると\(a\)になるのは\(+\sqrt{a}\)と\(-\sqrt{a}\)なので
\(a\)の平方根\(=±\sqrt{a}\)
ということになる。
つまり、
\((a\)の平方根\()^2=(±\sqrt{a})^2=a\)
こんな感じになる。
これが平方根の性質。
数学Ⅰは実数の範囲で考えるので、ルートの中は必ず正の数か\(0\)になる。
 平方根とは
平方根とは
例えば、\(\sqrt{2}\)を考えてみると
\(2\)の平方根\(=±\sqrt{2}\)
なので、
・\(\sqrt{2}\)は、\(2\)の平方根の\(+\sqrt{2}\)と\(-\sqrt{2}\)のうちの一つである「\(+\sqrt{2}\)」
ということになる。
2乗の場合を考えるときも同じ感じ。
2乗すると\(a^2\)になる数を「\(a^2\)の平方根」と呼ぶ。
\(a^2\)の平方根\(=±\sqrt{a^2}\)
こんな感じ。
例えば、\(\sqrt{3^2}\)を考えてみると
\(3^2\)の平方根\(=±\sqrt{3^2}\)
なので、
・\(\sqrt{3^2}\)は、\(3^2\)の平方根の\(+\sqrt{3^2}\)と\(-\sqrt{3^2}\)のうちの一つである「\(+\sqrt{3^2}\)」
ということになる。 \(3^2=9\)より
\(\sqrt{3^2}=\sqrt{9}\)
となり、2乗すると\(9\)になる数の\(-3\)と\(+3\)のうちの一つである「\(+3\)」を表しているので、
\(\sqrt{9}=3\)
となる。
この
\(\sqrt{3^2}=3\)
となるところが、ルートの中に2乗があるときはルートをそのまま外すという発想に辿り着く。

ルートの中に文字の2乗が入っている場合、「文字がプラスのとき」と「文字がマイナスのとき」を考えなければならない。
実際に数字を入れて考えてみる。
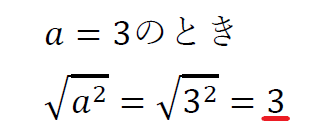
文字がプラスのときは、ルートを外したあとプラスになる。
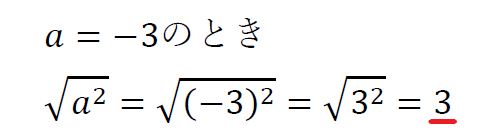
マイナスの2乗はプラスなので、
文字がマイナスのときも、ルートを外したあとプラスになる。
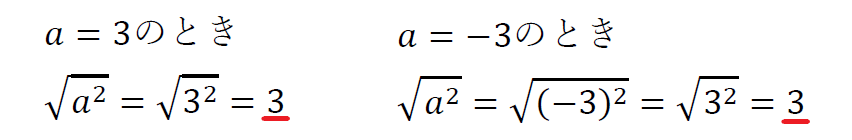
こんな感じに、「+3の2乗」でも「-3の2乗」でも、
ルートが外れた数字は必ず「プラス」になる。
これは、絶対値の性質と同じになる。
絶対値の性質は、
絶対値記号の中がマイナスのとき、絶対値記号の中に-1を掛ける。
これをルートで考えると、

こんな感じになる。
これを、絶対値の性質と同じということもまとめて表すと、

これが「ルートの中に文字の2乗があるときの性質」となる。
文字と言っても実際に数字を入れて具体的な値を求めることもできる。
その時は、その数字がプラスかマイナスかを判断して絶対値記号を外せばいい。

こんな感じ。
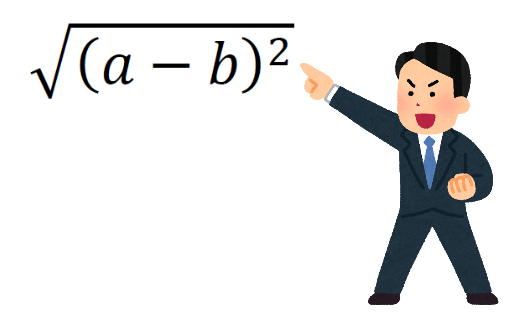
ルートの中に式の2乗が入っている場合、「式がプラスのとき」と「式がマイナスのとき」を考えなければならない。
実際に数字を入れて考えてみる。

ルートの中の式の2乗がプラスのときを考える。
式の2乗といっても、「ルートの中に文字の2乗があるときの性質」の式、

これを使うことで、式の2乗のパターンにも当てはめることができる。
つまり、aに式自体を代入して絶対値を考えれば良き。

こんな感じ。

ルートの中の式の2乗がマイナスのときを考える。
こちらも、「ルートの中に文字の2乗があるときの性質」の式、

に式ごと代入して考える。

こんな感じになる。

ルートの中に「2乗」が入っていたときは要注意。
絶対値の性質
絶対値記号の中がマイナスのとき、絶対値記号の中に-1を掛ける。

結構忘れがちな平方根の性質。
ルートの中が2乗だからといって、
単純にルートを取り払うことはできない。
こういう細かいところを理解しておくとケアレスミスも減る。
まずはルートの中身がプラスなのかマイナスなのかを確認する。
 すうがくのいえ
すうがくのいえ